Среди этих чисел не может быть числа, оканчивающегося на 0, так как на 0 не делится никакое число.
Значит, эти числа либо от до , либо от до .
Значит, в любом случае среди этих чисел есть следующие:
, делящееся на 2
, делящееся на 3
, делящееся на 4
, делящееся на 5
, делящееся на 6
, делящееся на 7
, делящееся на 8
Рассмотрим утверждение "" делится на 4"". Число делится на 4, если число, образованное двумя последними цифрами делится на 4. Значит делится на 4, делится на 4, делится на 4, делится на 2, значит - четное.
Рассмотрим утверждение "" делится на 3"". Число делится на 3, если сумма цифр числа делится на 3. Значит, делится на 3, делится на 3. Выпишем пары цифр, где , а - четное, в сумме кратные 3: (1; 2); (1; 8); (2; 4); (3; 0); (3; 6); (4; 2); (4; 8); (5; 4); (6; 0); (6; 6); (7; 2); (7; 8); (8; 4); (9; 0); (9; 6).
Рассмотрим утверждение "" делится на 7"". Если делится на 7, то делится на 7, делится на 7. Из ранее выписанных пар только пары (4; 2); (8; 4) удовлетворяют этому условию.
Мы учили делимость на 3, 4 и 7. Делимость на 2, 5 и 6 будет выполняться автоматически. Проверим делимость на 8. Число 428 не делится на 8, а число 848 делится на 8.
Число 841, очевидно, делится на 1, а число 849 не делится на 9. Значит, это числа от 841 до 848, а сумма цифр наименьшего числа равна 8+4+1=13.
Бесстрашная, энергичная, запасливая. Самая маленькая птица на земном шаре — колибри. Это одно из самых красивых творений природы. Достаточно только перечислить названия, которыми наградили эту птицу "топазный колибри", "изумрудное горлышко"," летающий аметист" и "огненный топаз". Колибри — самые маленькие из всех птиц. Самый крупный вид, гигантский колибри (Patagona gigas) из южноамериканских Анд, достигает величины 22 см. А самый мелкий вид, колибри — карликовая пчелка (Mellisuga minima) с острова Куба, достигает в длину всего лишь 6 см (от кончика хвоста до кончика клюва!); это самая маленькая птица на свете. В целом насчитывается 350 видов колибри, и все они живут в Америке, причем не только в тропиках и субтропиках, но и в других климатических зонах, вплоть до Аляски.
Среди этих чисел не может быть числа, оканчивающегося на 0, так как на 0 не делится никакое число.
Значит, эти числа либо от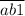
до 
, либо от 
до 
.
Значит, в любом случае среди этих чисел есть следующие:
Рассмотрим утверждение ""
делится на 4"". Число делится на 4, если число, образованное двумя последними цифрами делится на 4. Значит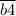 
делится на 4, 
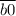делится на 4, 
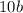делится на 4, 
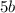делится на 2, значит 
- четное.
Рассмотрим утверждение ""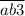
делится на 3"". Число делится на 3, если сумма цифр числа делится на 3. Значит, 
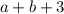делится на 3, 
делится на 3. Выпишем пары цифр, где 
, а 
- четное, в сумме кратные 3: (1; 2); (1; 8); (2; 4); (3; 0); (3; 6); (4; 2); (4; 8); (5; 4); (6; 0); (6; 6); (7; 2); (7; 8); (8; 4); (9; 0); (9; 6).
Рассмотрим утверждение ""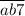
делится на 7"". Если 
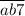делится на 7, то 
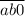делится на 7, 
делится на 7. Из ранее выписанных пар только пары (4; 2); (8; 4) удовлетворяют этому условию.
Мы учили делимость на 3, 4 и 7. Делимость на 2, 5 и 6 будет выполняться автоматически. Проверим делимость на 8. Число 428 не делится на 8, а число 848 делится на 8.
Число 841, очевидно, делится на 1, а число 849 не делится на 9. Значит, это числа от 841 до 848, а сумма цифр наименьшего числа равна 8+4+1=13.
ответ: 13