На малюнку 10 AD=AB, DC=CB. Доведіть:
а) ∆ADC=∆ABC;
б) AC – бісектриса кута BAD.
На малюнку 14 AB=CD, AC=BD. Доведіть рівність трикутників ABD і DCA.
На малюнку 15 AB=CD, BF=CE, AE=FD. Доведіть, що трикутник EOF рівнобедрений.
На малюнку 10 AD=AB, DC=CB. Доведіть:
а) ∆ADC=∆ABC;
б) AC – бісектриса кута BAD.
На малюнку 14 AB=CD, AC=BD. Доведіть рівність трикутників ABD і DCA.
На малюнку 15 AB=CD, BF=CE, AE=FD. Доведіть, що трикутник EOF рівнобедрений.
На малюнку 10 AD=AB, DC=CB. Доведіть:
а) ∆ADC=∆ABC;
б) AC – бісектриса кута BAD.
На малюнку 14 AB=CD, AC=BD. Доведіть рівність трикутників ABD і DCA.
На малюнку 15 AB=CD, BF=CE, AE=FD. Доведіть, що трикутник EOF рівнобедрений.
На малюнку 10 AD=AB, DC=CB. Доведіть:
а) ∆ADC=∆ABC;
б) AC – бісектриса кута BAD.
На малюнку 14 AB=CD, AC=BD. Доведіть рівність трикутників ABD і DCA.
На малюнку 15 AB=CD, BF=CE, AE=FD. Доведіть, що трикутник EOF рівнобедрений.
На малюнку 10 AD=AB, DC=CB. Доведіть:
а) ∆ADC=∆ABC;
б) AC – бісектриса кута BAD.
На малюнку 14 AB=CD, AC=BD. Доведіть рівність трикутників ABD і DCA.
На малюнку 15 AB=CD, BF=CE, AE=FD. Доведіть, що трикутник EOF рівнобедрений.
На малюнку 10 AD=AB, DC=CB. Доведіть:
а) ∆ADC=∆ABC;
б) AC – бісектриса кута BAD.
На малюнку 14 AB=CD, AC=BD. Доведіть рівність трикутників ABD і DCA.
На малюнку 15 AB=CD, BF=CE, AE=FD. Доведіть, що трикутник EOF рівнобедрений.
На малюнку 10 AD=AB, DC=CB. Доведіть:
а) ∆ADC=∆ABC;
б) AC – бісектриса кута BAD.
На малюнку 14 AB=CD, AC=BD. Доведіть рівність трикутників ABD і DCA.
На малюнку 15 AB=CD, BF=CE, AE=FD. Доведіть, що трикутник EOF рівнобедрений.
На малюнку 10 AD=AB, DC=CB. Доведіть:
а) ∆ADC=∆ABC;
б) AC – бісектриса кута BAD.
На малюнку 14 AB=CD, AC=BD. Доведіть рівність трикутників ABD і DCA.
На малюнку 15 AB=CD, BF=CE, AE=FD. Доведіть, що трикутник EOF рівнобедрений.
На малюнку 10 AD=AB, DC=CB. Доведіть:
а) ∆ADC=∆ABC;
б) AC – бісектриса кута BAD.
На малюнку 14 AB=CD, AC=BD. Доведіть рівність трикутників ABD і DCA.
На малюнку 15 AB=CD, BF=CE, AE=FD. Доведіть, що трикутник EOF рівнобедрений.
Пошаговое объяснение:
а) При значении а = -6 уравнение имеет корень равный 2.
При значении а = 16 уравнение имеет корень равный -3/4.
При значении а = 60 уравнение имеет корень равный -0,2.
b) При значении а = 0 уравнение не имеет корней.
c) При а > 0 уравнение будет иметь отрицательный корень.
Пошаговое объяснение:
Требуется найти, при каких значениях а уравнение
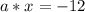 :
:
а)
1. Имеет корень, равный 2.
Подставим вместо х его значение 2 и решим уравнение относительно а:
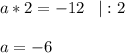
⇒ При значении а = -6 уравнение имеет корень равный 2.
2. Имеет корень, равный 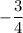 .
.
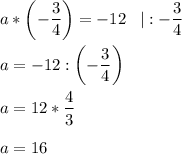
⇒ При значении а = 16 уравнение имеет корень равный 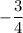 .
.
3. Имеет корень, равный -0,2.
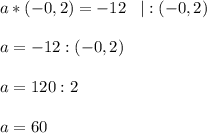
⇒ При значении а = 60 уравнение имеет корень равный -0,2.
b) Не имеет корней.
Уравнение не имеет решения, если при любом значении х, мы не получим верного равенства.Это возможно только тогда, когда а = 0.
Проверим:
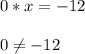
⇒ При значении а = 0 уравнение не имеет корней.
с) Имеет отрицательный корень.
Правая часть у нас отрицательная.
При нахождении корня, мы делим правую часть на а. Чтобы корень был отрицательным, то а должно быть положительным.
При делении чисел с разными знаками, частное - отрицательно.⇒ а > 0
⇒ При а > 0 уравнение имеет отрицательный корень.
BH=AB•sin30=(дробь 10 в числители 1/2 в знаменателе) =20 см
S=20•10=200 см2