Папа сказал что он идёт со скоростью 6км/ч на машине едет в 10раз быстрее а на велосипеде в 4 раза медленнее чем на машине с каокй скоростью папа едет на велосипеде с планом

👇

Увидеть ответ

Ответ:

aedilsultanova

01.10.2022

6•10=60[папа едет на м.]
60÷4=15(км/ч на вёл.)

4,6(86 оценок)

Открыть все ответы

Ответ:

DisasterYt

01.10.2022

Есть такое правило разрядных единиц: при умножении десятичных дробей на десять/100/1000 (все, что без запятой и с ноликами) запятая уходит, а при делении влево. С разрядными единицами (0,1/0,01/0,00001) наоборот.

То есть, чтобы из десятичной дроби получить число с нулями без запятой нам сначала нужно избавиться от запятой.

При умножении на разрядную единицу уйдет столько цифр после запятой, сколько ноликов. Если мы умножим 0,75 на 10, то получим 7,5, а если на 100 - 75.

В числе 750000 четыре нуля, но нельзя забывать, что число 0,75 у нас запятой, если мы умножим на просто 10.000, то получим 7500, потому что два нолика мы потратили на освобождение от запятой. Значит, нам нужно число с шестью нулями, это будет 1.000.000, другими словами миллион. Именно умножив 0,75 на него мы получим 750000.

А теперь вернемся к другим разрядным единицам (0,1/0,0001..). Умножение и деление на них действует противоположно 10. То есть, если мы умножаем на 0.1, то запятая будет уходить не вправо, а влево. Но зато при делении запятая поползет куда надо. Правило с этой разрядной единицей таково: запятая настолько уйдет вправо или влево, сколько цифр находится после запятой. Если у нас есть 0.1 и мы умножаем на нее 4, то получим 0.4, потому что после нуля стоит одна цифра (единица), а если мы умножим 4 на 0.01, то получим уже 0.04.

Чтобы получить из 0.75 нужное число, нам надо делить на разрядную единицу 0.000001, ведь два нолика мы тратим на освобождение от запятой, причем ноликов всего пять, ведь шестой цифрой будет единица.

Значит, у этого примера есть два решения: 0.75 * 0.000001 = 750.000

и 0.75 * 1.000.000

4,5(27 оценок)

Ответ:

JamesBond007007007

01.10.2022

x∈ (-n-2;-n+2]

Пошаговое объяснение:

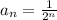
$a_n=\frac{1}{2^n}$

Вычислим радиус сходимости:

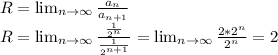
$R= \lim_{n \to \infty} \frac{a_n}{a_{n+1}}\\R= \lim_{n \to \infty} \frac{\frac{1}{2^n} }{\frac{1}{2^{n+1}} } = \lim_{n \to \infty} \frac{2*2^n}{2^n}=2$

Находим область сходимости степенного ряда:

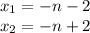
$x_1=-n-2\\x_2=-n+2\\$

x∈(-n-2; -n+2)

Остаётся проверить сходимость ряда на концах данного интервала.

При х = -n-2 мы получим следующий ряд:

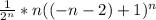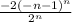
∑ $\frac{1}{2^n}*n((-n-2)+1)^n$ =∑ $\frac{-2(-n-1)^n}{2^n}$

Рассмотрим первых 3 члена данного ряда: -2; 1/8; -128

Данный ряд будем исследовать по признакам Лейбница

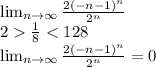
$\lim_{n \to \infty} \frac{2(-n-1)^n}{2^n} \\2\frac{1}{8}$

Как видим, выполняется лишь второе условие Лейбница, а значит ряд расходится => x=-n-2 является точкой расходимости.

Рассматриваем второй конец x=-n+2

Получаем следующий ряд

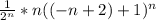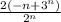
∑ $\frac{1}{2^n}*n((-n+2)+1)^n$ =∑ $\frac{2(-n+3^n)}{2^n}$

Тут исследуем по признакам Даламбера

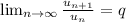
$\lim_{n \to \infty} \frac{u_{n+1}}{u_n}=q$

q=1 - неопределённость, т.к. при q>1 ряд расходится, а при q<1 - сходится.

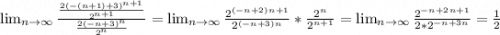
$\lim_{n \to \infty} \frac{\frac{2(-(n+1)+3)^{n+1}}{2^{n+1}} }{\frac{2(-n+3)^n}{2^n} }= \lim_{n \to \infty} \frac{2^{(-n+2)}^{n+1}}{2^{(-n+3)}^n} *\frac{2^n}{2^{n+1}}= \lim_{n \to \infty} \frac{2^{-n+2}^{n+1}}{2*2^{-n+3}^n} =\frac{1}{2}$