Question

Основанием пирамиды является прямоугольный треугольник с катетами, равными 6 и 8 см. каждый из двугранных углов, образованных боковыми гранями и основанием пирамиды, равен 60° найти площадь боковой поверхности пирамиды.

Answer 1

надо провести высоту пирамиды.

Проведем DO — высоту пирамиды и перпендикуляры DK, DM и DN к соответствующим сторонам ΔАВС.

по теореме о трех перпендикулярах OK ⊥ ВС, ОМ ⊥ АС и ON ⊥ AB. Где ∠DKO = ∠DMO = ∠DNO = 60° — линейные углы данных двугранных углов.

следовательно, треугольники DKO, DMO и DNO равны по катету и острому углу. Тогда OM = OK = ON, то есть точка О является центром окружности, вписанной в основание.

по теореме пифагора в прямоугольном ΔAВС:

$AB=\sqrt{AC^2+BC^2}=\sqrt{6^2+8^2}=\sqrt{100}=10$

найдем площадь ΔAВС

S=1/2*АС*АВ=1/2*6*8=24 кв см

с другой стороны S=pr=24/112= 2 см

тогда ΔDMO

DO=MO*tg60=r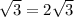$\sqrt{3}=2\sqrt{3}$ Нашли высоту пирамиды

Теперь надо по теореме пифагора найти высоты боковых граней в ΔDКO

DO^2+OK^2=DK^2

$DK=\sqrt{2^2+(2\sqrt{3})^2}=\sqrt{4+12}=\sqrt{16}=4$

Sобщ= Sabc+Sabd+Sacd+Sbcd=24+1/2*6*4+1/2*8*4+1/2*10*4=

=24+12+16+20=72 кв см

 если только боковая, то

Sбок =Sabd+Sacd+Sbcd=1/2*6*4+1/2*8*4+1/2*10*4=

=12+16+20=48 кв см