Сразу скажу, что условие скорей всего неправильное. Для такой задачи треугольник должен был быть равнобедренным. Но если это не так, то я решила по тому условию, которое Вы дали:
Есть 2 варианта решения этой задачи.
1) если стороны, о которых идёт речь - катеты
тогда 1 катет - а, второй - 11а
тогда гипотенуза: корень из (121a^2+a^2) =а*корень из 122
получаем:
a+11a+a*корень из 22 = 144
а*(1+11+корень из 122)=144
a=144/(12+корень из 122) (это одна сторона)
тогда вторая сторона: 144*11/(12+корень из 122)=1584/(12+корень из 122)
третья: (144*корень из 122)/(12+корень из 122)
2) если одна сторона - катет, пусть он будет a, вторая гипотенуза 11а
тогда третья сторона : корень из (121а^2-a^2)=а*(корень из 120)= 2а*корень из 30
составляем уравнение:
a+11a+2a*корень из 30 = 144
12а+2а*корень из 30 = 144
2а(6+корень из 30) = 144
а=144/(2*(6+корень из 30)) = 72/(6+корень из 30)
тогда вторая сторона 72*11/(6+корень из 30)= 792/(6+корень из30)
третья сторона ( 144*корень из30)/(6+корень из 30)
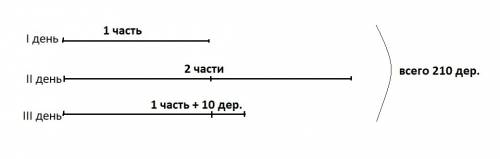
Решение по действиям: (см. схему в приложении)
1) 210 - 10 = 200 дер. - уравняли все части
2) 1 + 2 + 1 = 4 части - всего
3) 200 : 4 = 50 дер. - 1 часть (или в I день)
4) 50 * 2 = 100 дер. - во II день
5) 50 + 10 = 60 дер. - в III день
ответ: в I день посадили 50 деревьев, во II день 100 деревьев, а в III - 60 деревьев.
Решение уравнением:
х дер. - в I день
2х дер. - во II день
х + 10 - в III день
1) х + 2х + (х + 10) = 210
4х + 10 = 210
4х = 200
х = 50 дер. - в I день
2) 2х = 2 * 50 = 100 дер. - во II день
3) 50 + 10 = 60 дер. - в III день