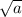, то необходимо домножить и числитель, и знаменатель на этот корень (основное свойство дроби)
или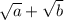 
, то числитель и знаменатель необходимо домножить на сопряжённое выражение (для первого: на 
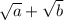; для второго выражения на 
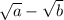), сведя числитель к формуле разности квадратов. Это алгоритм для квадратных корней. Для корней больше 2 степени сопряжённые ищутся иначе и по другим формулам.
1) Фигура, принадлежащая пересечению множеств А и В - это фигура, обладающая одновременно свойствами множества А и множества В. Такими свойствами обладает прямоугольный равнобедренный треугольник. (см. вложение)
2) Если А – множество однозначных чисел, В – множество нечётных натуральных чисел, меньших 19, то объединение этих множеств - множество, в котором находятся все однозначные числа и нечетные натуральные числа, меньшие 19.
A={0,1,2,3,4,5,6,7,8,9}
B={1,3,5,7,9,11,13,15,17,}
А∪В={1,2,3,4,5,6,7,8,9,11,13,15,17}
3) см. вложение.
