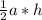
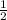 a · b · sin γ
a · b · sin γ 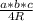
г 1: находим координаты х точек перечечения графиков y=x^2+1 и y=-x+3.
x^2+1 = -x+3; x^2+x-2 = 0; x1 = -2; x2 = 1.
Шаг 2: Находим определенный интеграл функции y = -x+3 в пределах от -2 до 1.
Первообразная этой функции будет Y = -1/2*x^2 + 3x + С
Подставляя пределы интегрирования получаем площадь под функцией S1 = -1/2 + 3 + 2 + 6 = 10,5.
Шаг 3: Находим определенный интеграл функции y = x^2+1 в пределах от -2 до 1.
Первообразная этой функции будет Y = 1/3*x^3 + x + С
Подставляя пределы интегрирования получаем площадь под функцией S2 = 1/3 + 1 + 8/3 +2 = 6.
Шаг 4: S = S1-S2; S = 10,5-6; S = 4,5.
Пошаговое объяснение:
2) периметр квадрата равен сумме всех сторон т.е. 5 + 5 + 5 + 5 = 20
3) найдем стороны прямоугольника:
т.к. периметры квадрата и прямоугольника равны получаем
2 * (4х + х) = 20 (где х - меньшая сторона прямоугольника)
5х = 10
х = 2
Меньшая сторона прямоугольника равна 2 см
большая сторона равна 4 * 2 = 8 см
4) площадь прямоугольника равна 8 * 2 = 16 см2
5) периметр прямоугольника равен 20 см (смотри выше)