5*11+4=59
проверка
59:11=5 5*11=55 59-55=4
Древние славяне обычно строили свои поселения по берегам рек. Вода была необходима для жизни и ведения хозяйства, а кроме того, реки использовались и как торговые пути. Через древнюю Русь проходил один из старинных торговых путей «из варяг в греки».
Он начинался на реке Неве, по которой корабли входили в Ладожское озеро. Из Ладожского озера по реке Волхов плыли до озера Ильмень, на берегу которого находился Новгород, один из древнейших русских городов. От Новгорода по большим и малым рекам добирались до Днепра, а дальше плыли до Киева, а оттуда уже было близко до Черного моря.
Трудность плавания, в котором необходимо преодолевать волоком два водораздела — между Ловатью и Двиной и между Двиной и Днепром. Причем расстояние по маршруту Балтика-Волхов-Ловать-Двина-Днепр (с двумя волоками) в 5 раз больше, чем по маршруту Балтика-Двина-Днепр (с одним волоком), проходящему через города Рига, Полоцк и Смоленск. Существует и не менее удобный путь Балтика-Висла-Буг-Припять-Днепр (также с одним волоком), проходящий через города Плоцк, Брест, Пинск и Туров, сразу выходящий в район Киева, функционирующий и в настоящее время.
Трудность плавания, в котором необходимо преодолевать волоком два водораздела — между Ловатью и Двиной и между Двиной и Днепром. Причем расстояние по маршруту Балтика-Волхов-Ловать-Двина-Днепр (с двумя волоками) в 5 раз больше, чем по маршруту Балтика-Двина-Днепр (с одним волоком), проходящему через города Рига, Полоцк и Смоленск. Существует и не менее удобный путь Балтика-Висла-Буг-Припять-Днепр (также с одним волоком), проходящий через города Плоцк, Брест, Пинск и Туров, сразу выходящий в район Киева, функционирующий и в настоящее время.
Удобные водные пути развитию торговых связей Киевской Руси с другими государствами Европы и Азии. Ведь по рекам можно было добраться до Волги, а оттуда через Каспийское море и до Средней Азии.
Плавание по рекам тогда было трудным и опасным. Древнерусским судам - ладьям — приходилось преодолевать и каменистые участки — пороги, и по сухопутным путям волоком добираться от одной реки до другой. Но русские купцы не боялись далеких путешествий и вели интенсивную торговлю. Вот почему уже к концу Х века новгородские гости - так тогда называли купцов из-за их мирных намерений, связанных только с желанием торговать, - освоили почти весь русский Север от берегов Финского залива до самого Урала.
Русские купцы вывозили в Западную Европу меха и кожи, «рыбьи зубы», так тогда назывались моржовые клыки, а также лен, сало и мед. Обратно везли серебро и медь, стекло, различные изделия из золота, ткани и оружие.
Особенно активно торговали с Русью купцы из северных немецких городов, их называли варяжскими гостями, поскольку варягами русские люди называли каждого человека, который приплыл к ним из-за моря.
Трудность плавания, в котором необходимо преодолевать волоком два водораздела — между Ловатью и Двиной и между Двиной и Днепром. Причем расстояние по маршруту Балтика-Волхов-Ловать-Двина-Днепр (с двумя волоками) в 5 раз больше, чем по маршруту Балтика-Двина-Днепр (с одним волоком), проходящему через города Рига, Полоцк и Смоленск. Существует и не менее удобный путь Балтика-Висла-Буг-Припять-Днепр (также с одним волоком), проходящий через города Плоцк, Брест, Пинск и Туров, сразу выходящий в район Киева, функционирующий и в настоящее время.
![t^2 - 8 t + [7-a] = 0 ,](/tpl/images/0495/7941/4dac0.png) где под
где под 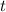 подразумевается квадрат переменной
подразумевается квадрат переменной 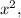 т.е.
т.е.  а его корнями
а его корнями 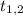 – квадраты искомых корней, если они различны, или его чётным корнем
– квадраты искомых корней, если они различны, или его чётным корнем 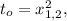 если корень биквадратного трёхчлена
если корень биквадратного трёхчлена 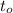 – единственный.
– единственный.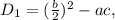 тогда
тогда ![D_1 = 4^2 - [7-a] = 9 + a .](/tpl/images/0495/7941/d229f.png) Потребуем, чтобы
Потребуем, чтобы 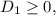 откуда следует, что
откуда следует, что 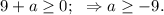
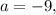 а корень биквадратного трёхчлена станет чётным
а корень биквадратного трёхчлена станет чётным  давая два искомых корня
давая два искомых корня 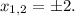 Это значение
Это значение 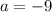 как раз уже и есть одно из искомых решений для параметра
как раз уже и есть одно из искомых решений для параметра 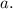
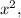 всегда будет два – левый и правый (меньший и больший), однако при некоторых обстоятельствах левый квадрат искомых корней будет отрицательным, а значит, не будет давать пару искомых корней. Среднеарифметическое квадратов искомых корней
всегда будет два – левый и правый (меньший и больший), однако при некоторых обстоятельствах левый квадрат искомых корней будет отрицательным, а значит, не будет давать пару искомых корней. Среднеарифметическое квадратов искомых корней 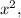 по теореме Виета, в применении к биквадратному уравнению, будет равно числу, противоположному половине среднего коэффициента, т.е. оно равно
по теореме Виета, в применении к биквадратному уравнению, будет равно числу, противоположному половине среднего коэффициента, т.е. оно равно 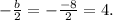 Отсюда следует, что правый квадрат искомых корней
Отсюда следует, что правый квадрат искомых корней 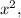 – всегда положителен, а значит, всегда даёт два корня при положительном дискриминанте.
– всегда положителен, а значит, всегда даёт два корня при положительном дискриминанте.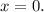 А значит, значение всего трёхчлена
А значит, значение всего трёхчлена ![x^4 - 8 x^2 + [7-a]](/tpl/images/0495/7941/7bbf9.png) взятое от
взятое от 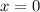 должно давать отрицательное значение, т.е. располагается в нижней межкорневой дуге параболы биквадратного трёхчлена.
должно давать отрицательное значение, т.е. располагается в нижней межкорневой дуге параболы биквадратного трёхчлена.![0^4 - 8 \cdot 0^2 + [7-a] < 0](/tpl/images/0495/7941/13440.png) ;
; ;
;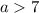 ;
;
Насколько я понял задание то это число 59 .