1. надо продифференцировать числитель и знаменатель и потом вычислить предел, производная числителя равна 12х+13, а знаменателя 6х+8, можно еще раз продифференцировать числитель и знаменатель, , в числителе получим 12, в знаменателе 6, значит, предел равен 12/6=2 2.Ко второму примеру применить правило Лопиталя нельзя, т.к. предел отношения двух бесконечно малых величин должен быть равен пределу отношения их производных, если последний предел существует, но это не так. предел не существует.
3. найдем производные числителя и знаменателя, а потом возьмем предел при х стремящемся к к нулю. (2cos2х)/(2sin2x)=ctg2x, а
предел ctg2x, если х устремить к нулю, равен ∞
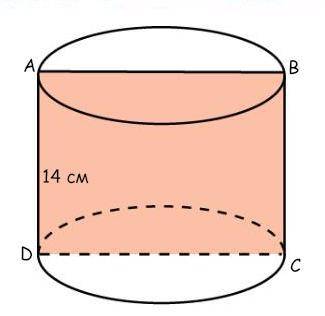
Если в цилиндре осевое сечение - квадрат, то радиус основания в два раза меньше образующей. Образующая цилиндра равна высоте.
Как и сказала, радиус основания = 1/2 * 14 см = 7 см.
А объём цилиндра равен произведению площади основания на высоту.
То есть :
V(цилиндра) = (7 см)²*14 см*π = 686 см³*π.
ответ : 686 см³*π.Задача №3.Брусок имеет форму прямоугольного параллелепипеда.
Находим объём чугунного бруска. Он равен произведению трёх его измерений :
V(чугунного бруска) = 5,5 см*20 см*40 см = 4400 см³.
А массу найдём по этой формуле :
m = p*V
Где m - масса тела, p - плотность вещества, из которого изготовлено тело, V - объём тела.
Подставляем и считаем :
m = (7,5 г/см³) * 4400 см³ = 33000 г = 33 кг.
ответ : 33 кг.