 , лежит на перпендикуляре, проведённым из точки А к этой прямой.
, лежит на перпендикуляре, проведённым из точки А к этой прямой. можно провести в плоскости, перпендикулярной прямой
можно провести в плоскости, перпендикулярной прямой  .
. будет нормальным вектором плоскости и точка А лежит в этой плоскости.
будет нормальным вектором плоскости и точка А лежит в этой плоскости.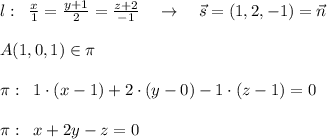
 и плоскости
и плоскости 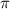 .
. 
 является серединой отрезка
является серединой отрезка 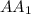 .
.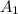 .
.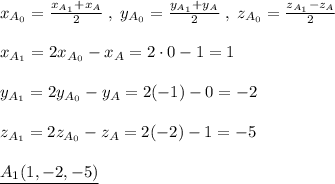
1-я сторона = 5 частей,
2-я = 7 частей,
3-я = 11 частей.
Сумма самой большей и самой меньшей сторон = 80, т.е., нужно посмотреть, какая сторона имеет самое большее количество частей, и какая сторона имеет самое меньшее кол-во частей.
В данной задаче самая большая сторона имеет 11 частей, а самая маленькая имеет 5 частей. Нужно сложить эти части: 5+11=16(ч.)
То есть, эти 16 частей равны 80 см, а чтобы узнать, сколько см содержится в одной части, нужно 80:16= 5 (см). Теперь найдем ту часть, которая содержит 7 частей : 7*5= 35 (см).
Теперь мы знаем сумму 1-й и 3-й стороны, и только что вычислили длину 2-й стороны. Чтобы найти периметр, нужно сложить все стороны: Р=80+35=115(см)
ответ: Р=115см