Дано:
S = 203 км - расстояние АВ.
m = 100 км/ч - скорость второго
t1 = 3 ч - время задержки второго
Найти: Sc = ? - расстояние АС.
Пошаговое объяснение:
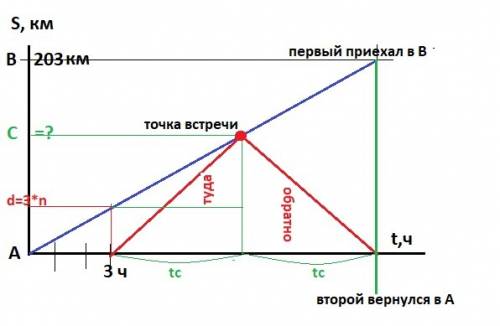
Делаем схему движения - рисунок в приложении. n - скорость первого.
Постановка задачи: АС = m*tc = 110*tc. Найти - tc- время "погони".
Можно написать такие уравнения:
1) d = n*t1 = 3*n - дистанция "погони" - первый "убежал".
2) tc = d/(m-n) - время до встречи "погони"
3) T = S/n = 203/n - время в пути первого - прибыл в пункт В.
4) Т = 3 + 2*m*tc - одновременно - первый прибыл в пункт В, а второй вернулся в пункт А.
Пробуем составить окончательное уравнение.
5) 203/n = 3 + 2*3*n/(110-n)
203/n = 3 + 6*n/(110-n)
6) 203*(110-n) = 3*n*(110-n) + 6n²
7) 22330 - 203*n = 330*n - 3n² + 6n²
8) 3*n² - 127*n - 22330 = 0
Решаем квадратное уравнение и получаем:
D = 284089, √D = 533, и два корня: n1 = 110 и УРА - n = 67 2/3 (≈67.(6))
Дальше не решается, где-то ошибки, но может быть подсказка
Пошаговое объяснение:
Перевод :
"Два оператора,работая совместно могут набрать текст рукописи на компьютере за 10 ч. Они совместно набрали текст 6 ч , затем первый оператор набрал оставшуюся часть текста за 12 ч. За сколько часов набрал бы весь текст рукописи первый и второй оператор?"
Вся рукопись это 1 ( целая)
Если два оператора набирают всю рукопись на 10 часов , то за 6 часов они набрали :
6 : 10 =6/10 = 3/5 части рукописи
Осталось набрать
1 - 3/5 = 2/5 часть рукописи и на это у первого оператора ушло 12 часов , значит всю рукопись он может набрать за:
12 : 2/5 = 12 * 5 : 2 = 30 часов
За 10 часов совместной работы он бы набрал :
30 часов - 1
10 часов - х
х= 10 : 30 = 1/3 часть всей рукописи , значит второй оператор за это же время набрал :
1- 1/3 = 2/3 части всей рукописи
Значит всю рукопись второй оператор набрал бы за :
2/3 части - 10 часов
1 ( целая) - х часов
х= 1*10 : 2/3 = 10* 3/2 = 15 часов
ответ : первый оператор , весь текст , наберет за 30 часов , второй за 15 часов