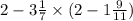
Сначала для удобства переведём дроби в неправильные:
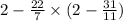
Теперь поочерёдно начнём выполнять действия. Первым действием является скобка. Перед тем, как выполнить вычитание, нужно привести оба числа в одинаковому знаменателю, для этого умножим 2 на 11 и после этого вычтем:
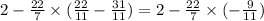
Следующим действием является умножение. Обе дроби являются отрицательными, значит их произведение будет положительным, так как при умножении минуса на минус бужет плюс. Сократим и умножим:
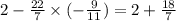
Осталось выполнить последнее действие, которым является сложение. Для начала приведём эти числа к общему знаменателю, сложим и выделим целую часть:
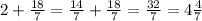
Вот и ответ.
90 - уменьшаемое
х - вычитаемое
53 + 10 - сумма чисел (разница)
Уравнение: 90 - х = 53 + 10
90 - х = 63
х = 90 - 63
х = 27
- - - - - - - - - - - - - - - - - - - - - - - - - - -
90 - уменьшаемое
х - вычитаемое
6 · 5 - произведение чисел (разница)
Уравнение: 90 - х = 6 · 5
90 - х = 30
х = 90 - 30
х = 60
- - - - - - - - - - - - - - - - - - - - - - - - - - -
90 - уменьшаемое
х - вычитаемое
32 : 4 - частное чисел (разница)
Уравнение: 90 - х = 32 : 4
90 - х = 8
х = 90 - 8
х = 82
--(cosx -- sinx) = 2cosx(cosx -- sinx) , сокращаем скобки и получаем
--1 = 2 cosx или сosx = --1\2
x = +_ arccos(--1\2) + 2Пn = +_ ( П -- arccos1\2) +2Пn = +_ (П -- П\3) + 2Пn =
= +_ 2П\3 + 2Пn = 120° + 2Пn
n∈Z