Пусть все 290 слагаемых равны по 2. Тогда их сумма равна 290·2=580, что меньше 2020. Значит, среди слагаемых есть число, большее 2.
Пусть каждое из 290 слагаемых равно по 2 или по 3. Тогда максимальная сумма, даваемая с таких слагаемых равна 290·3=870, что меньше 2020. Значит, среди слагаемых есть число, большее 3.
Пусть каждое из 290 слагаемых равно по 2, по 3 или по 5. Тогда максимальная сумма, даваемая с таких слагаемых равна 290·5=1450, что меньше 2020. Значит, среди слагаемых есть число, большее 5.
Пусть каждое из 290 слагаемых равно по 2, по 3, по 5 или по 7. Тогда максимальная сумма, даваемая с таких слагаемых равна 290·7=2030. Это больше, чем 2020, значит такой вариант можно рассматривать далее.
Максимальная сумма получается при суммировании 290 чисел, каждое из которых равно по 7. Как видно, максимальная сумма больше требуемой на 10. Тогда, можно уменьшить некоторые слагаемые в этой сумме. Например, уменьшить 2 слагаемых на 5. Получим сумму вида:
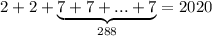
Наибольшим слагаемым является число 7.
ответ: 7
Очевидно, что 17 крестиков поставить на доску с такими условиями невозможно.
16 крестиков поставить на доску также невозможно. Если предположить, что такое случилось, то единственная пустая клетка разобьет доску на два ряда крестиков. Но по условию ряда из 8 крестиков быть не должно, значит длина каждого из двух рядов не более 7, а значит общее число крестиков не более 14. Но мы предполагали, что расставляем на доску 16 крестиков. Противоречие.
Для 15 крестиков можно показать требуемую расстановку:
XX XX XX XO XX XX XX XO X, где X - крестик, O - пустая клетка
ответ: 15
х*(х-4)=96
х(в квадрате)-4х=96
х(в квадрате)-4х-96=0
а=1 в=-4 с=-96 к=-2
D1=4+96=100
2+;-10
х1;2=
1
х1=12
х2=-8
выбираем ответ 12, т.к. сторона не может быть отрицательным числом. это будет первая сторона, обозначенная за х.
вторая сторона на 4см. меньше другой, поэтому она будет равняться:
12-4=8см.
можно сделать проверку:
96=8*12
ответ: 8см, 12см. (еще надо учесть, что параллельные стороны равны).