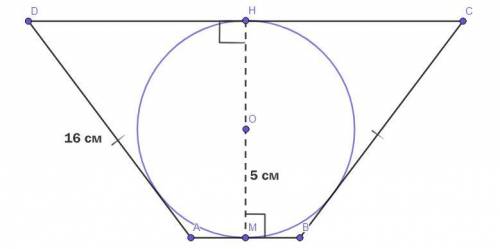
Дано :
Четырёхугольник ABCD - равнобедренная трапеция (AB║DC, AD = BC).
Окружность с центром О - вписанная в равнобедренную трапецию окружность.
ОМ - радиус окружности = 5 см.
AD = BC = 16 см.
Найти :
S(ABCD) = ?
Если в четырёхугольник можно вписать окружность, то суммы противоположных сторон равны.
Следовательно -
AD + BC = AB + DC.
Но так как -
AD = BC = 16 см.
Поэтому -
AD + BC = 16 см + 16 см = 32 см
AB + DC = 32 см.
Радиус вписанной в трапецию окружности равен половине высоты.
На чертёже НМ - высота ABCD, следовательно -
НМ = 2*ОМ
НМ = 2*5 см
НМ = 10 см.
Площадь трапеции равна произведению полусуммы оснований и высоты.
То есть -
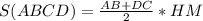
Теперь в формулу подставляем известные нам численные значения и считаем -
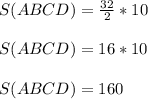
ответ : 160 (ед²).

Денис разбил треугольник на девять треугольничков, как показано на рисунке,
и расставил в них числа, при этом в белых треугольниках числа оказались
равны суммам чисел в соседних с ними (по сторонам) серых треугольниках,
После этого Леша стер числа 1, 2, 3, 4, 5 и 6 и вместо них написал буквы А, В,
C, D, E и Fв некотором порядке. Получившаяся расстановка чисел и букв
изображена на рисунке.
Где какие числа стояли первоначально?
Для создания пары сперва нажмите на одну из строк левого столбца, а затем
на необходимую строку в правом. Каждой строке в левом столбце соответствует
ровна одна строка в правом.