1 картинка: 46,6048
2 картинка: 113,04
Пошаговое объяснение:1 картинка:Площадь окружности равна 2π · r²(Для сокращения буду писать So)
Площадь прямоугольника ab(a и b - стороны)(S)
Площадь заштрихованной фигуры равна S-So
So=2π · r²=2π · 2,2²=2 · 3,14 · 4,84=6,28 · 4,84=30,3952
S=ab=7 · 11=77
S-So=77 - 30,3952=46,6048
2 картинка:(Я правильно понимаю, что эти окружности имеют общий центр?)
Обозначим радиус большей окружности R, а меньшей r
R=r + 3=1,5 + 3=4,5
Площадь окружности 2π·r²(Буду писать S для площади большей из окружностей, а s для площади меньшей)
Площадь заштрихованной фигуры S-s
S=2π · R²=2 · 3,14 · 4,5²=2 · 3,14 · 20,25=6,28 · 20,25=127,17
s=2π · r²=2 · 3,`14 · 1,5²=2 · 3,14 · 2,25=6,28 · 2,25=14,13
S-s=127,17 - 14,13=113,04
Неравенство ax² + bx + c < 0 не будет иметь решений, если парабола
y = ax² + bx + c будет расположена над осью Ох или будет касаться оси.
Для этого коэффициент а должен быть положительным, а уравнение ax² + bx + c = 0 не должно иметь корней или иметь один корень, т.е. дискриминант должен быть меньше либо равен нулю:
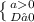
(p - 1) x² + (p - 2) x + 3p - 1 < 0
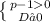
D = (p - 2)² - 4(p - 1)(3p - 1) = p² - 4p + 4 - 12p² + 16p - 4 = - 11p² + 12p
- 11p² + 12p ≤ 0
p(11p - 12) ≥ 0 (см. рис. 1)
p ∈ (- ∞ ; 0] ∪ [12/11 ; + ∞)
p > 1
(см. рис. 2)
p ∈[12/11 ; + ∞)
3/2 : Х = 19/4 : 19/8
3/2 : Х = 19/4 : 8/19
3/2 : Х = (19*8)/(4*19) (сокращаешь)
3/2 : Х = 2/1
3/2 : Х = 2
Х = 3/2 : 2
Х = 3/2 : 1/2
Х = 3/4
ответ: