ΔАВС - равнобедренный , АВ=АС ⇒ ∠В=∠АСВ .
Рассм. ΔADE. Чтобы доказать, что АЕ>AD , надо доказать, что ∠ADE>∠AED , так как против бОльшего угла лежит бОльшая сторона .
Рассм. ΔBDF. Внешний угол этого треугольника ∠ADF=∠ADE равен сумме двух углов треугольника, не смежных с ним, то есть
∠ADE=∠B+∠BFD , но ∠В=∠АСВ ⇒ ∠ADE=∠ACB+∠BFD .
Но ∠АСВ - это внешний угол ΔCEF , и поэтому ∠ACB=∠CEF+∠CFE .
Значит, ∠ADE=∠CEF+∠CFE+∠BFD .
Но ∠CFE - это тот же самый угол, что и ∠BFD , ∠CFE=∠BFD .
∠ADE=∠CEF+2*∠CFE
∠CEF=∠AED как вертикальные углы, поэтому
∠ADE=∠AED+2*∠CFE
То есть один ∠ADE равен одному ∠AED плюс ещё два угла ∠CFE , значит ∠ADE>∠AED и сторона, лежащая против ∠ADE (сторона АЕ) больше стороны, лежащей против ∠AED (сторона AD).
AE>AD
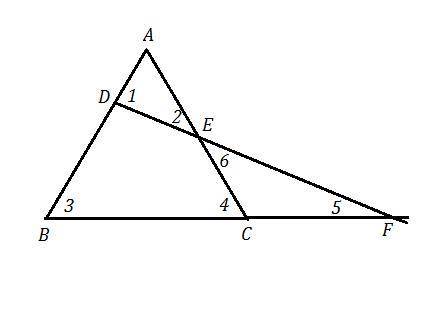
Или запись короче, если обозначить углы, как на рисунке:
∠1=∠3+∠5=∠4+∠5=(∠6+∠5)+∠5=∠6+2*∠5=∠2+2*∠5 ⇒
∠1=∠2+2*∠5 , ∠1 >∠2 ⇒ АЕ>AD .
Пошаговое объяснение:
1)3/7 + 5/6=18/42+35/42=1 11/42
2) 11/12 - 7/8=22/24-21/24=1/24
3)5/9 : 10/27=5/9*27/10=3/2=1 1/2
4)1 8/25 * 1 4/11=33/25*15/11=9/5=1 4/5
5)5/14 * 7/30=1/12
6) 4 4/9 : 1 2/3=40/9*3/5=8/3=2 2/3
(x+2 5/6):20 + 7 1/5= 7 1/2
(x+2 5/6):20 =- 7 1/5+ 7 1/2
(x+2 5/6):20 =7 5/10-7 2/10
(x+2 5/6):20=3/10
Х+2 5/6=3/10*1/20
Х+2 5/6=3/200
Х=3/200-2 5/6
Х=9/600-2 500/600
Х=-2 491/600
4 5/9-2 5/6=4 10/18-2 15/18=1 13/18 кг
во втором ящике
4 5/9+1 13/18=4 10/18+1 13/18=5 5/18 кг в двух ящиках
Х:7=4 5/7
Х=4 5/7*7
Х=33/7*7
Х=33
7/а, при а = 8, 9, 10, 11, 12 , 13, 14, 15 и т. д.