ответ: x=2-t
y=-3+4*t
z=4-2*t,
(x+2)/-1=(y+3)/4=(z-4)/-2.
Пошаговое объяснение:
Так как прямая параллельна вектору а, то данный вектор является для этой прямой направляющим. Обозначим через x0, y0 и z0 координаты точки А, а через a, b и c - координаты вектора а. Параметрические уравнения прямой в пространстве имеют вид:
x=x0+a*t
y=y0+b*t
z=z0+c*t
Подставляя известные координаты точки и направляющего вектора, получаем систему параметрических уравнений:
x=2-t
y=-3+4*t
z=4-2*t
Для составления канонического уравнения нужно найти из этой системы выражения для параметра t через x, y и z:
t=(x+2)/-1, t=(y+3)/4, t=(z-4)/-2. Приравнивая эти три выражения, получаем каноническое уравнение:
(x+2)/-1=(y+3)/4=(z-4)/-2.
Пошаговое объяснение: Первый шаг: сократи в левой части уравнения восьмёрку и четвёрку, получаем: 2(2х+7)=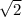
/2
Второй шаг: Умножаем обе части уравнения на 2, чтобы избавиться от знаменателя: 4(2х+7)=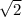
Третий шаг: Раскрываем скобки в правой части уравнения: 8х+28=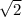
Четвёртый шаг: возводим обе части уравнения в квадрат: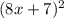 
=2
Пятый шаг: Раскрываем скобки в левой части уравнения: 64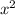
+112
+49=2
Приводим квадратное уравнение к стандартному виду: 64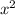+112+47=0
Находим дискриминант:D=12544-12032=512
1=-112+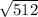
/128=(-7+16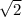)/8
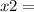-112-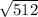/128=(-7-16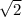)/8
