Пошаговое объяснение:
Различают следующие виды случайных событий: достоверные, невозможные и случайные. События обозначаются большими латинскими буквами А, В, С,...,Z. Достоверное событие всегда происходит в результате наблюдения или испытания. Достоверное событие обозначается символом – W.
Невозможное событие никогда не происходит в результате наблюдения или испытания. Невозможное событие обозначается символом – Æ.
Пример. Если в корзине только персики, то достать из корзины персик является достоверным событием, а достать лимон является невозможным событием.
Случайное событие – это такое событие, которое в результате наблюдения или испытания может произойти, а может и не произойти.
Пример. Студент сдаёт экзамен. Экзамен сдан. Это событие случайное, так как студент мог и не сдать экзамен.
Кроме того, события могут быть совместными и несовместными, зависимыми или независимыми. Два события называются совместными, если появление одного из них не исключает появления другого в одном и том же испытании. Примеры совместных событий: два стрелка стреляют по мишени, два спортсмена одновременно бегут. Случайные события А и В называются несовместными, если при данном испытании появление одного из них исключает появление другого события. Несовместные события: день и ночь, студент одновременно едет на занятие и сдаёт экзамен, число иррациональное и чётное.
Событие А называется независимым от события В, если вероятность появления события А не зависит от того произошло событие В или нет. Пример. Два студента одновременно сдают экзамен независимо друг от друга. Это событие совместное и независимое. Событие А называется зависимым от события В, если вероятность появления события А зависит от того произошло или не произошло событие В. Пример. Работник получит оплату труда в зависимости от качества её выполнения.
Равновозможные события – это такие события, которые имеют одинаковые возможности для их появления. Полная группа событий – это совокупность единственно возможных событий при данном испытании. Пример. Студент может сдать экзамен на любую оценку. В данном случае возможны следующие события: студент может сдать экзамен на 5, студент может сдать экзамен на 4, студент может сдать экзамен на 3. Эти события образуют полную группу.
Противоположные события. Два случайные события А и В называются противоположными, если они несовместны и образуют полную группу событий. Примеры: студент может сдать или не сдать экзамен, день и ночь.
Конкретный результат испытания называется элементарным событием. Совокупность всех возможных, различных, конкретных исходов испытаний называется множеством элементарных событий.
Сложным событием (исходом) называется произвольное подмножество множества элементарных событий. Сложное событие в результате испытания наступает тогда и только тогда, когда в результате испытаний произошло элементарное событие, принадлежащее сложному. Например, испытание – подбрасывание кубика. Элементарное событие – выпадение грани с числом «5». Сложное событие – выпадение грани с нечётным числом.
х (км/ч) - скорость течения реки
(20 - х) км/ч - скорость катера против течения
(20 + х) км/ч - скорость катера по течению
Тогда время, затраченное на путь против течения равен:
36/(20 - x) ч
А время пути по течению реки:
22/(20 + x) ч
Составим уравнение:
36/(20 - x) + 22/(20 + x) = 3
36/(20 - x) + 22/(20 + x) - 3 = 0 x ≠ 20, x ≠ - 20
720 + 36x + 440 - 22x - 3 * (20² - x²) = 0
1 160 + 14x - 1 200 + 3x² = 0
3x² + 14x - 40 = 0
D = 14² - 4 * 3 * (- 40) = 196 - (- 480) = 676
= 
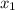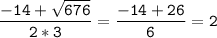км/ч
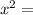
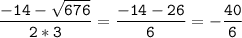- не подходит под условие
ответ: скорость течения реки равна 2 км/ч.
4 * b - 16 = 10 * 2 = 20
4 * b = 20 + 16 = 36
b = 36 : 4 = 9
(2 + x : 7) * 8 = 72
2 + x : 7 = 72 : 8 = 9
x : 7 = 9 - 2 = 7
x = 7 * 7 = 49
35 : (15 - y : 8) = 5
15 - y : 8 = 35 : 5 = 7
y : 8 = 15 - 7 = 8
y = 8 * 8 = 64
(t * 3 + 5) : 4 = 8
t * 3 + 5 = 8 * 4 = 32
t * 3 = 32 - 5 = 27
t = 27 : 3 = 9