Question

Логарифмы. решить неравество. подробнее. пример в приложении

Answer 1

$2log_8(x-2)-log_8(x-3)\frac{2}{3}\; \; ODZ\, :\; \left \{ {{x2} \atop {x3}} \right.\; \; \Rightarrow \; \; \underline {x3}\\\\log_8(x-2)^2-log_8(x-3)\frac{2}{3}\\\\log_8\frac{(x-2)^2}{x-3}log_88^{\frac{2}{3}}\; \; ,\; \; 8^{\frac{2}{3}}=\sqrt[3]{8^2}=\sqrt[3]{2^6}=2^2=4\\\\\frac{(x-2)^2}{x-3}4\; \; ,\; \; \frac{x^2-4x+4-4(x-3)}{x-3}0\; \; ,\; \; \frac{x^2-8x+16}{x-3}0\; \; ,\; \; \frac{(x-4)^2}{x-3}0\; ,\\\\znaki\, :\; \; \; ---(3)+++(4)+++\\\\x\in (3,4)\cup (4,+\infty )$

$\left \{ {{x3\qquad \qquad } \atop {x\in (3,4)\cup (4,+\infty )}} \right. \; \; \; \Rightarrow \; \; \; \underline {x\in (3,4)\cup (4,+\infty )}$

Answer 2

$x 3$

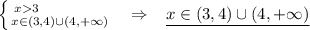
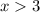
Пошаговое объяснение:

ОДЗ:

$x - 2 0 \\ x - 3 0 \\ \\ x 2 \\ x 3 \\ \\ x 3$

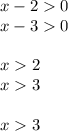
Внесём 2 в степень:

$log_{8}({(x - 2)}^{2} ) - log_{8}(x - 3) \frac{2}{3}$

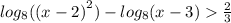
По свойству степени:

$log_{8}( \frac{ {(x - 2)}^{2} }{x - 3} ) \frac{2}{3}$

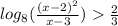
Возведём 8 в эти степени

А т.к. 8>1, то знак неравенства не поменяется:

${8}^{ log_{8}( \frac{ {(x - 2)}^{2} }{x - 3} ) } {8}^{ \frac{2}{3} }$

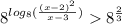
По определению логарифма:

$\frac{ {(x - 2)}^{2} }{x - 3} \sqrt[3]{ {8}^{2} }$

$\frac{ {(x - 2)}^{2} }{x - 3} - 4 0$

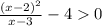
Внесём в дробь -4:

$\frac{ {(x - 2)}^{2} - 4x + 12}{x - 3} 0 \\ \frac{{x}^{2} - 4x + 4 - 4x + 12 }{x - 3} 0 \\ \frac{ {x}^{2} - 8x + 16}{x - 3} 0 \\ \frac{ {(x - 4)}^{2} }{x - 3} 0$

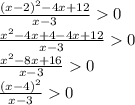
Числитель всегда больше либо равен нуля значит надо потребовать чтобы знаменатель был больше нуля

И числитель должен быть не равен нулю:

x≠4

$x - 3 0$

$x 3$

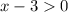
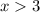
С учётом ОДЗ, А ОНО У НАС:

x>3

x€(3;4)U(4;+бесконечности)

Я старался! :)