Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Пусть один из внутренних углов, не смежных с внешним, имеет градусную меру в х градусов. Тогда второй не смежный угол имеет меру в (х + 10) градусов.
Найдём внешний угол, опираясь на то, что сумма всех углов треугольника равна 180°: 230° - 180° = 50°.
Составим уравнение:
х + (х + 10) = 50
2х + 10 = 50
2х = 40
х = 20
20° + 10° = 30° (второй угол, не смежный с внешним)
180° - 20° - 30° = 130° (третий угол, смежный с внешним)
ответ: 20°, 30° и 130°.
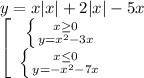
y=x²-3x.
Это парабола, ветви которой вверх. Найдём точки пересечения с осями координат: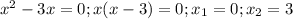 
(0;0) и (3;0)
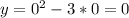(0;0).
Вершина параболы: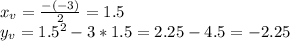 
(1.5;-2.25)
y=-x²-7x
Это парабола, ветви которой вниз. Найдём точки пересечения с осями координат: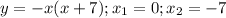 
(-7;0) и (0;0)
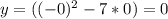(0;0).
Вершина параболы: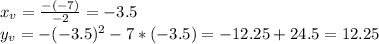 
(-3.5;12.25)
Сначала построим графики отдельно, отметим ограничение и построим в общей системе координат.
Прямая y=m, это прямая, которая параллельна оси Ох, по графику функции видно, что сначала 1 пересечение, потом 2, затем 3, опять 2 и снова 1 пересечение. Две общие точки, когда два пересечения, а именно в вершинах, парабол, которые мы строили до этого, нам нужно значение по ординате, поэтому берём -2.25 и 12.25.
ответ: m={-2.25;12.25}
12.8*10.4=133.12