Прямая, которая задается уравнением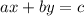 
, можно переписать в виде функции 
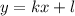, где 
Определим формулу линейной функции, которая проходит через две точк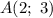и: 
и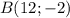 
Для этого подставим соответствующие координаты точек в функцию и получим систему из двух линейных уравнений:
Из первого уравнения 
подставим во второе уравнение:
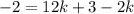
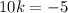
Тогда 
Получили линейную функцию, которая задается формулой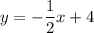 
Для проверки того, проходит ли прямая через заданную точку, следует подставить координаты этой точки в функцию и посмотреть результат.
а) Для точки 
:
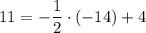
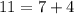— правда
б) Для точки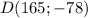 
:
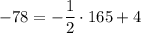
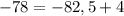
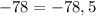— неправда
ответ: а) да; б) нет.
длина окружности Р=2
R
а) Р=2*3,14*2,1=13,188 (см)
б) R=1/2D=15:2=7,5
Р=2*3,14*7,5=47,1 (см)