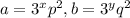, где p и q - натуральные числа, не делящиеся на 3. Ясно, что x<n, y<n. Если x=y, то, разделив обе части на 
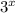, получим уравнение 
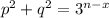. Поскольку числа p и q не делятся на 3, а величина n-x больше 0, это уравнение корней не имеет. Наконец, рассмотрим случай, когда x≠y, в силу симметрии можно считать, что x<y. Разделив уравнение на 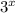, имеем 
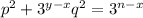. Первое слагаемое не делится на 3, второе и третье делятся, получили противоречие.
ответ: 1/2*ln/{[√(x²+1)-1]/[√(x²+1)+1]}/+C.
Пошаговое объяснение:
Подынтегральное выражение имеет вид x^m*(a*x^n+b)^p*dx, где m=-1, n=2, p=-1/2, a=b=1. Такое выражение называется дифференциальным биномом и интегрируется в конечном виде только в трёх случаях:
1) если p - целое число;
2) если (m+1)/n - целое число;
3) если (m+1)/n+p - целое число.
Очевидно, что мы имеем второй случай, так как (-1+1)/2=0 - целое число. В этом случае производится замена переменной по формуле a*x^n+b=t^M, где M - знаменатель числа p. В нашем случае M=2, поэтому применяем подстановку x²+1=t². Отсюда x²=t²-1, x=√(t²-1) и dx=t*dt/√(t²-1). После подстановки выражений для x, √(x²+1) и dx подынтегральное выражение принимает вид dt/(t²-1), и тогда искомый интеграл I(t)=∫dt/(t²-1)=1/2*ln/(t-1)/(t+1)/. Отсюда I(x)= 1/2*ln/{[√(x²+1)-1]/[√(x²+1)+1]}/+C.
