Числа A и B называются взаимно простыми, если НОД(А; В)=1.
Возможны различные варианты :
а) Если числа А и В простые, то НОД(А; В)=1. Например:
НОД(2; 3)=1, НОД(2; 5)=1, НОД(3; 7)=1.
1) 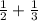
Так как НОД(2; 3)=1, то НОК(2; 3)=2·3=6
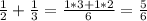
2) 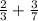
НОД(3; 7)=1, то НОК(3; 7)=3·7=21
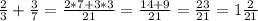
б) Если числа А и В составные, но не имеют одинаковых простых делителей, тогда НОД(А; В)=1. Например:
НОД(4; 9)=1, НОД(4; 25)=1, НОД(9; 16)=1.
3) 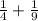
Так как НОД(4; 9)=1, то НОК(4; 9)=4·9=36
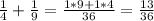
2) 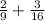
НОД(9; 16)=1, то НОК(9; 16)=9·16=144
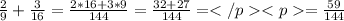
В общем случае, если А и В взаимно простые, то есть
НОД(А; В)=1, то НОК(А; В)=А·В.
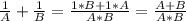
R=√S/π=√49/3,14=√15,6≈√16≈4 см