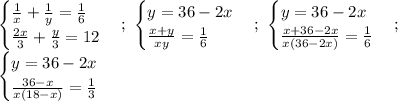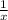Найти 1 третия часть числа 25674 и 3 четвёртая часть от 23764

👇

Увидеть ответ

Ответ:

zima21zima

16.05.2022

1)25674:3=8558;/// 2)23764:4*3=17823

4,6(96 оценок)

Ответ:

masha20321

16.05.2022

1/3 от 25674=8558
3/4 от 23764=17823

4,7(36 оценок)

Открыть все ответы

Ответ:

donamigo2012

16.05.2022

Комментарий. В задаче говорится, что у грузовиков разная грузоподъемность. Это условие влечет за собой разное время выполнения целого задания этими грузовиками при самостоятельной работе.

Пусть х ч - требуется I грузовику, а у ч - II грузовику для перевозки груза при самостоятельной работе.
Тогда $\frac{1}{x}$ раб/ч - производительность I грузовика,
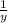$\frac{1}{y}$ раб/ч - производительность II грузовика
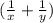$(\frac{1}{x} + \frac{1}{y})$ раб/ч - производительность грузовиков при совместной работе, которая по условию равна 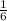$\frac{1}{6}$ раб/ч.
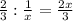$\frac{2}{3}: \frac{1}{x} = \frac{2x}{3}$ ч - затратил I грузовик на выполнение 2/3 работы.
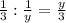$\frac{1}{3}: \frac{1}{y} = \frac{y}{3}$ ч - затратил II грузовик на выполнение 1/3 работы.
По условию, работая друг за другом, оба грузовика справились с заданием за 12 ч.
Получаем систему уравнений:
$\begin {cases} \frac{1}{x} + \frac{1}{y}= \frac{1}{6} \\ \frac{2x}{3} + \frac{y}{3}=12 \end {cases};\ \begin {cases} y= 36-2x \\ \frac{x+y}{xy} = \frac{1}{6} \end {cases} ;\ \begin {cases} y= 36-2x \\ \frac{x+36-2x}{x(36-2x)} = \frac{1}{6} \end {cases};\ \\ \begin {cases} y= 36-2x \\ \frac{36-x}{x(18-x)} = \frac{1}{3} \end {cases}$
108-3x=18x-x²
x²-21x+108=0
D= 441-432 = 9
x=12 или х=9
Если х=12, то у=36-2*12=12
Если х=9, то у=36-2*9=18
В силу сказанного выше в комментарии, условию задачи удовлетворяет пара х=9, у=18.
Значит, 9 ч требуется I грузовику, 18 ч требуется II грузовику.
ответ: 9 ч, 18 ч.
Два автомобиля с различной грузоподъемностью должны были перевезти некоторый груз за 6 часов. второй

Два автомобиля с различной грузоподъемностью должны были перевезти некоторый груз за 6 часов. второй

4,4(76 оценок)

Ответ:

1Haritoshka

16.05.2022

Пусть нам удалось включить наибольшее возможное количество лампочек. Рассмотрим конфигурацию лампочек и выключателей, которая получилась в результате переключений. Разобьем все выключатели на группы A и B. В первой группе находятся выключатели, которые переключали нечетное число раз, во второй находятся переключатели, переключенные четное число раз (или вообще не переключавшиеся). Рассмотрим произвольную лампочку x между двумя выключателями из A. Суммарно выключатели, смежные с этой лампочкой, переключались четное число раз (сумма двух нечетных чисел), поэтому в итоге лампочка окажется выключенной. Аналогично, рассмотрим произвольную лампочку y между двумя выключателями из B. Два смежных с ней выключателя также переключались четное число раз, поэтому лампочка в итоге тоже останется выключенной. Теперь рассмотрим произвольную лампочку z между двумя выключателями из разных групп. Поскольку суммарно смежные с ней выключатели переключателись нечетное число раз, эта лампочка будет гореть. Таким образом, гореть будут те и только те лампочки, которые находятся между переключателями из разных групп.

Пусть в группе A находится 10-k выключателей, а в группе B 10+k. Тогда существует (10-k)(10+k) лампочек, на концах которых находятся выключатели из разных групп. Таким образом, достаточно найти наибольшее возможное значение выражения (10-k)(10+k) при условии 0≤k≤10. Очевидно, (10-k)(10+k)=100-k²≤100. Таким образом, одновременно могут гореть не более 100 лампочек.

Примечание: логичнее рассмотреть группы из k и 20-k лампочек, но тогда для нахождения максимального значения нужно брать производную, что выходит за рамки 9 класса.

4,8(46 оценок)

Это интересно:

Стиль-и-уход-за-собой

03.12.2020

Безопасность в городе: как защитить себя от хулиганов?...

Дом-и-сад

21.02.2022

Как выращивать тыкву зимних сортов: советы и рекомендации...

Кулинария-и-гостеприимство

27.12.2021

Как готовить морского окуня: секреты профессионалов...

Питомцы-и-животные