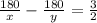
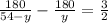
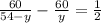
дано:
ромб авсе,
ан — высота,
вн = нс,
ав = 6 сантиметров,
найти площадь ромба s авсе — ?
решение:
1) рассмотрим прямоугольный треугольник авн.сторона вн = нс = 1/2 * 6 = 6/2 = 3 (сантиметра). по теореме пифагора (квадрат гипотенузы равен сумме квадратов катетов):
ан^2 + вн^2 = ав^2 (выразим из данного равенства катет ан^2);
ан^2 = ав^2 - вн^2;
ан^2 = 6^2 - 3^2;
ан^2 = 36 - 9;
ан^2 = 27;
ан = √27;
ан = 3√3;
2) рассмотрим ромб авсе.
s авсе = ан * вс;
s авсе = 3√3 * 6;
s авсе = 18√3 сантиметров квадратных.
ответ: 18√3 сантиметров квадратных.
А)1/2 и 1/3; (2*3=6-произведение знаменателей. Числитель и знаменатель первой дроби умножим на 3, второй дроби на 2)
1/2=3/6 и 1/3=2/6
Б)1/2=5/10 и 1/5=2/10;
В) 1/2=7/14 и 1/7=2/14;
Г) 1/2=9/18 и 1/9=2/18;
Д) 1/2=3/6 и 6/12=6/12;
Е) 1/2=5/10 и 3/5=6/10;
Ж) 1/2= 7/14 и 6/7=12/14;
З) 1/2 =9/18 и 7/9=14/18;
И) 1/7=8/56 и 1/8=7/56;
К) 3/7=24/56 и 5/8=35/56;
Л) 1/10=11/110 и 1/11=10/110;
М) 3/10=33/110 и 10/11=100/110;
Н) 1/10=13/130 и 1/13=10/130;
О) 1/10=13/130 и 2/13=20/130;
П) 3/10=39/130 и 4/13=40/130;
Р) 9/10=117/130 и 12/13=120/130