5875 или 8575
Пошаговое объяснение:
Полное условие: Четырёхзначное число называется восхитительным, если оно само делится на 25, его сумма цифр делится на 25 и его произведение цифр делится на 25. Найдите все восхитительные числа.
Решение. Представим четырёхзначное число x в виде :
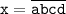, где a, b, c и d - цифры, причём a≥1.
Применим признак делимости на 25:
Число делится на 25 тогда и только тогда, когда две его последние цифры составляют число, которое делится на 25.
Другими словами, на 25 делятся числа, оканчивающиеся на 00, 25, 50 или 75.
Тогда искомое число может имеет 4 вида:
1) 
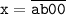
2) 
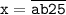
3) 
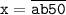
4) 
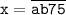
Для этих чисел проверим остальные условия:
1) .
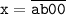Для суммы цифр числа выполняется неравенство
0<1+0+0+0≤a+b+0+0≤9+9+0+0=18<25, поэтому сумма цифр не делится на 25. Не подходит!
2) .
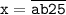Для суммы цифр числа выполняется неравенство
0<1+0+0+0≤a+b+2+5=a+b+7≤9+9+7=25.
Отсюда, сумма цифр только числа 9925 делится на 25.
Произведение цифр этого числа равно 810 и не делится на 25. Не подходит!
3) .
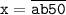Для суммы цифр числа выполняется неравенство
0<1+0+0+0≤a+b+5+0=a+b+5≤9+9+5=23<25, поэтому сумма цифр не делится на 25. Не подходит!
4) .
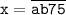Для суммы цифр числа выполняется неравенство
0<1+0+0+0≤a+b+7+5=a+b+12. Тогда должен выполнятся равенство:
a+b+12=25 или a+b=13. Отсюда видно, что a и b не равны.
Применим условие задачи "произведение цифр делится на 25". Произведение цифр равно a·b·7·5 и делится на 5. Так как a и b цифры, то для того, чтобы a·b·7·5 делился на 25 (=5·5), хотя бы один из множителей a или b должен делится на 5.
а) пусть a=5. Тогда из a+b=13 получаем, что b=13-5=8;
б) пусть b=5. Тогда из a+b=13 получаем, что a=13-5=8.
ответ: x=5875 или x=8575.
Пошаговое объяснение:
1. log₁₂160+log₁₂0,9=log₁₂(160*0,9)=log₁₂144=log₁₂12²=2*log₁₂12=2.
ответ: 1).
2. 5^ (2+log₅3)=5²*5^log₅3=25*3=75
ответ: 3).
3. 2*log₂12-log₂18=log₂12²-log₂18=log₂144-log₂18=log₂(144/18)=
=log₂8=log₂2³=3*log₂2=3.
ответ: 1).
4. log₄(16*c)=log₄16+log₄c=log₄4²+log(₂²)c=2*log₄4+(1/2)*log₂c=
=2+0,5*0,5=2+0,25=2,25.
ответ: 2).
5. (log₅144/log₅12)-8=(log₅12²/log₅12)-8=(2*log₅12/log₅12)-8=2-8=-6.
6. log₂(24*m)=log₂(8*3m)=log₂8+log₂3m=log₂2³+log₂3m=
=3*log₂2+8,5=3+8,5=11,5.
ответ: 1).
7. log₅(25/c)=log₅25-log₅c=log₅5²-(1/(log(c)5))=2*log₅5-(1/0,2)=1-5=-3.
ответ: 3).
8. 81^(log₃⁴√5)-2^log₀,₅5=3^(4*log₃⁴√5)-2^log₁/₂5=
3^log₃(⁴√5)⁴-2^(-log₂5)=3^log₃5-(1/(2^log₂5))=5-(1/5)=5-0,2=4,8.
ответ: 3).
1 тракторист за 1день 36:6=6 га
3 тракториста за 1 день 36*3=108 га
ответ: 108 га