Пошаговое Обозначим через а цифру десятков этого двузначного числа.
Тогда цифра единиц этого число должна быть равной 2а, само двузначное число можно будет записать в виде 10а + 2а = 12а, а то число, которое получается из исходного путем перестановки его цифр — в виде 2а * 10 + а = 20а + а = 21а.
В исходных данных к данному заданию сообщается, что полученное путем перестановки цифр число больше исходного на 27, следовательно, можем составить следующее уравнение:
21а = 27 + 12а,
решая которое, получаем:
21а - 12а = 27;
9а = 27;
а = 27 / 9 = 3.
Следовательно, искомое число это 36.
ответ: 36.объяснение:
Пошаговое объяснение:
можно, конечно, и просто считать, но лучше всего заполнить круги Эйлера
Ф - множество владеющих французским
А - множество владеющих английским
Н - множество владеющих немецким
итак, поехали
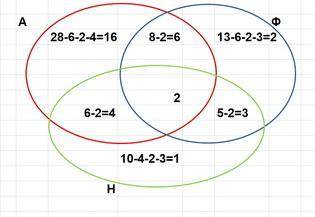
в самом центре пересечения всех кругов (множеств) запишем тех, кто знает 3 языка - это цифра 2
А ∩ Ф - это знающие английский и французский, таких 8, но 2 уже есть, поэтому запишем 8-2 = 6
А ∩ Н - это 6, опять же 2 уже есть значит 6-2 = 4
Ф ∩ Н - это 5, аналогично предыдущему запишем 5-2 = 3
и, наконец, сами множества владеющих языками
А - это 28-6-2-4 = 16 (от 28 отнимаем всех, кого уэе учли в предыдущих операциях)
Ф - это 13-6-2-3=2
Н - это 10-4-2-3= 1
теперь можем посчитать всех, владеющих языками
для этого сложим все циферьки в кругах и пересечениях кругов
16+6+2+4+2+3+1 = 34
и у нас еще есть 41 "безъязыких" участников группы
добавим их и получим ответ 34+41 = 75
ответ в группе 75 спортсменов
16 : 28 = 16/28 = 4/7 - отношение сдавших на "4" и "5" к количеству учеников в 6Б.
Приведем дроби 3/4 и 4/7 к общему знаменателю 28.
3/4 = 21/28
4/7 = 16/28
21/28 > 16/28, значит, успеваемость в 6А выше, чем в 6Б.