15 (км/час) - скорость туриста на велосипеде
Пошаговое объяснение:
Пусть скорость туриста на велосипеде = х км/час. Тогда скорость пешком = (х - 11) км/час.
За 2 часа пешком со скоростью (х -11) км/час турист путь = (х-11) *2 (км), а на велосипеде за один час он проехал расстояние = х * 1 (км)
Составим уравнение и найдём скорость туриста на велосипеде:
(х -11) * 2 + х * 1 = 23
2х - 22 + х = 23
3х = 23 + 22
3х = 45
х = 45 : 3
х = 15 (км/час) - скорость туриста на велосипеде
15 - 11 = 4 (км/час) - скорость туриста пешком
Проверка:
15 км/час * 1 час + 4 км/час * 2 = 15 км + 8 км = 23 км - общий путь туриста
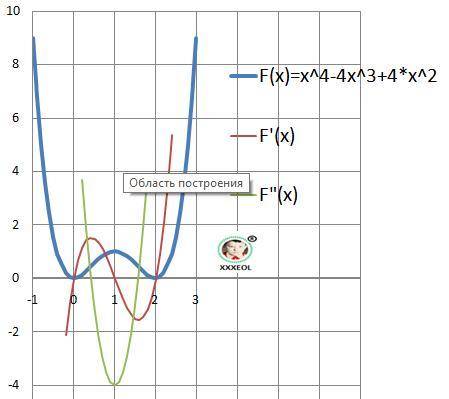
ДАНО: Y(x) = x⁴ - 4*x³+ 4*x² .
ИССЛЕДОВАНИЕ:
Описание ГЛАЗАМИ: Функция четвертого порядка с положительным коэффициентом - примерно парабола и ветви вверх. Должно быть четыре корня.
1. Область определения. Непрерывная. Разрывов нет.
D(x) = (-∞;+∞)
2. Нули функции - пересечение с осью ОХ.
Y= x²*(4*x²- 4*x +4) = 0
х₁ =0 и х₃ = 2 Двух других нет.
Пересечение с осью ОУ - Y(0) = 0/
3. Интервалы знакопостоянства/
Положительна: Y>0 X∈(-∞;0)∪(0;2)∪(2;+∞)
Y=0 X=(0;2) - в нулях функции. корней.
4. Поиск экстремумов по первой производная функции .
Y'(x) = 4*x³ -12*x² + 8x = 4*x*(x²- 12*x + 2) = 0
Точки экстремумов: x = 1, x = 2, x = 0
5 Локальные экстремумы:
Ymin(0) = Y(2) = 0, Ymax(1) = 1.
6. Интервалы монотонности.
Убывает: Х∈(-∞;0) ∪ (1;2)
Возрастает: Х∈(0;1) ∪ (2;+∞)
7, Поиск точек перегиба по второй производной
Y"(x) = 12*x² -24х +8 = 0
x₈ ≈ 0.42 и х₉ = 1.58 - точки перегиба.
8. Вогнутая - "ложка" - Х∈(-∞;0,42)∪(1.58;+∞) - вне корней.
Выпуклая - "горка" - Х∈(х₈=-0,42;1.58)
График на рисунке в приложении.
Гипотенуза * на высоту = произведению катетов.
5*h = 3*4
h= 12/5=
ответ: