x > 2
Пошаговое объяснение:
Данное неравенство равносильно следующей системе:
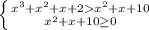
Первое неравенство системы - исходное, возведенное во вторую степень
Второе неравенство - ограничение на существование(т.к левая часть больше правой, которая неотрицательная, то условие на существование левой части можно не учитывать).
Запишем второе неравенство в виде уравнения и убедимся, что корней нет . Т.к. (D < 0), значит, парабола лежит выше оси Oy,следовательно, нет никаких ограничений на x.
В первом неравенстве системы получаем :
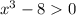 - разность кубов, которая раскладывается следующим образом:
- разность кубов, которая раскладывается следующим образом:
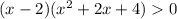
Второй множитель больше 0 при всех x из множества R, значит, достаточно, чтобы только x-2 > 0, то есть, x > 2
Находим пределы аргумента по заданным пределам функции.
у=1/х^2.
х = 1/+-√у.
х₁ = 1/√1 = 1.
х₂ = 1/(-√1) = -1
х₃ = 1/√4 = 0,5
х₄ = 1/(-√4) = -0,5.
В промежутке между х=-0,5 и х = 0,5, ограниченном линиями у=1 и у=4 функция представляет собой прямоугольник размером 1 на 3, S = 3.
Площадь криволинейного участка состоит из двух одинаковых площадей.
Достаточно найти одну из них и умножить на 2.
S = ∫₀.₅¹(1/x²)dx = (-1/x)|₀.₅¹ = -1/1 -(-1/0.5) = -1 + 2 = 1.
ответ: площадь функции,ограниченную линиями: у=1/х^2, у=1, у=4 равна S = 3 + 2*1 = 5.