Это простейшие производные.
Рассмотрим общий случай:
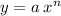
а – просто коэффициент при Х, n – степень Х.
Производная функции у, обозначаемая обычно у' или dy/dx, будет иметь следующий вид:
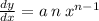
Ничего сложного.
Рассмотрим несколько частных случаев из Ваших примеров.
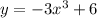
Здесь коэффициент а равен (–3), степень n равна 3. Значит, по правилу, представленному выше, производная будет иметь вид:
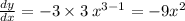
При числе 6 нет «Х», поэтому при взятии производной это число просто пропадает.
Другой частный пример:
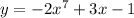
Берём производную от каждой части по отдельности.

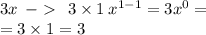

Итого:
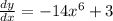
1) А)sin²α +cos²α =1 , т.к. cos α=-2\3 , α∈(π;3π\2) ,
sin²α +4\9 =1 , sin²α=5\9 , sinα=-√5\3 , т.к 3 четверть.
Б) tgх=sinх/cosх ⇒ tgх=(-2\3)/( -√5\3) =2\√5.
В) sin2α = 2•sinα•cosα ⇒sin2α =2*(-√5\3 )*(-2\3 )=4√5\9.
cos2α = cos²α − sin²α=4\9-5\9=-1\9.
2) А)sin²α +cos²α =1 , т.к. sinα=-0,6 , α∈(π;3π\2) ,
0,36+cos²α =1 , cos²α=0,64 , cosα=-0,8 , т.к 3 четверть.
Б) tgх=sinх/cosх ⇒ tgх=-0,6)/(-0,8) =3\4=0,75.
В) sin2α = 2•sinα•cosα ⇒sin2α =2*(-0,6)*(-0,8 )=0,96.
cos2α = cos²α − sin²α=0,64-0,36=0,28.
3)sin290•cos185*sin205•cos(-100)>0
sin290<0 т.к. 4 четверть , имеет знак -
cos185<0 т.к. 3 четверть , имеет знак -
sin205<0 т.к. 3 четверть , имеет знак -
cos(-100)<0 т.к. 3 четверть , имеет знак -
2)11/5+14/15=33/15+14/15=47/15*(-5/2)=-47/6=-7 5/6.