Объем полной поверхности правильной шестиугольной призмы равен 415,7 см3, а площадь 323,1 см2.
Пошаговое объяснение:
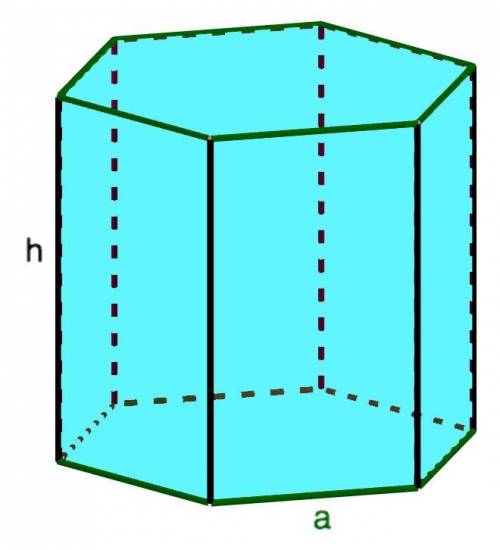
У правильной шестиугольной призмы основанием является правильный шестиугольник, где боковые грани перпендикулярны основаниям.
Объем правильной шестиугольной призмы равен произведению площади правильного шестиугольника, лежащего в основании, на высоту призмы, где высота призмы - это её боковое ребро.
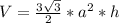
У нас боковое ребро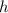 
равно 10 см, а ребро основания 
равно 4 см (как наглядно показано на рисунке). Подставляем и считаем:
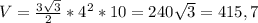см3.
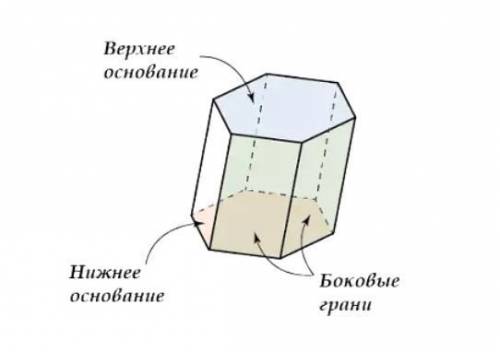
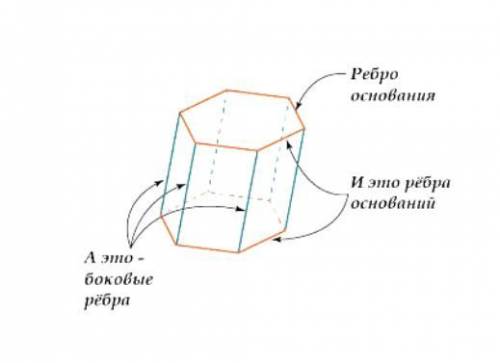
Правильная шестиугольная призма имеет два основания, где ее основания - правильные шестиугольники со стороной , и шесть боковых сторон, которые представляют из себя прямоугольники со сторонами и .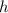
Поэтому площадь полной поверхности правильной шестиугольной призмы равна сумме площадей ее двух оснований и шести площадей боковых граней призмы.
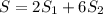
Где площадь основания находится согласно формуле:
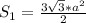
А площадь боковых граней равна: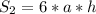 
Подставляя это в формулу общей площади получим:
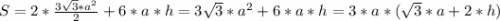
Подставляя наши значения получаем:
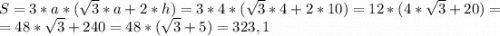см2.
Получаем ответ: объем полной поверхности правильной шестиугольной призмы равен 415,7 см3, а площадь 323,1 см2.
1) 3 руб, 5 руб.
2) х= -1 у= -5
Пошаговое объяснение:
1.
Пусть х руб. стоит карандаш, у руб. стоит ручка
составляем уравнения по условию задачи
х+у=8
5х+2у=25
выражаем в первом уравнении у через х
у=8-х и подставляем это выражение во второе уравнение
5х+2·(8-х)=25 решаем уравнение
5х+16-2х=25
3х=9
х=9÷3=3 руб. стоит карандаш
находим значение у
у=8-х=8-3=5 руб. стоит ручка
2.
2х-у=3
6х-2у=4
в первом уравнении выражаем у через х
у=2х-3 подставляем данное выражение во второе уравнение вместо у
6х-2·(2х-3)=4 решаем уравнение
6х-4х+6=4
2х=-2
х=-2÷2=-1
находим значение у
у=2х-3=2·(-1)-3=-5
просто между некоторыми знак не ставить.