Математика: 8y-3(2y-3)=7y-2(5y+8) найдите корень уравнения

8y-3(2y-3)=7y-2(5y+8) найдите корень уравнения

👇

Увидеть ответ

Ответ:

katemcgrat

28.09.2021

8y-3(2y-3)=7y-2(5y+8)

8y-6y-9=7y-10y-16

8y-6y-9-7y+10y+16=0

-11y=-7

y=7\11

4,5(27 оценок)

Ответ:

BOYKO10

28.09.2021

8y-3(2y-3)=7y-2(5y+8)

8y-6y+9=7y-10y-16

8y-6y-7y+10y = -16-9

5y=-25

y = -25 : 5

у = -5

ответ: -5

4,4(81 оценок)

Открыть все ответы

Ответ:

14sanka

28.09.2021

УМНОЖЕНИЕ
1. Произведение двух чисел не изменяется при перестановке множителей.
Это свойство умножения называют ПЕРЕМЕСТИТЕЛЬНЫМ. С букв его записывают так:
a+b=b+a
2. Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель.
Это свойство умножения называют сочетательным. С букв его записывают так:
a*(b*c)=(a*b)*c
3.Сумма n слагаемых, каждое из которых равно 1, равна n. Поэтому верно равенство 1*n=n
4. Сумма n слагаемых, каждое из которых равно нулю. Поэтому верно равенство 0*n=0
5.Чтобы переместительное свойство умножения было верно при n = 1 и n = 0, условились, что m*1=m и m*0=0.
6 Перед буквенными множителями обычно не пишут знак умножения: вместо 8 * x пишут 8x, вместо a*b пишут ab.
7. Опускают знак умножения и перд скобками. Например, вместо 2*(a+b) пишут 2(a+b), а вместо (x+2) * (y+3) пишут (x+2)(y+3) Вместо (ab)c пишут abc.
8.Когда в записи произведения нет скобок, умножение выполняют по порядку слева направо.

4,5(65 оценок)

Ответ:

Alexsandar

28.09.2021

Задачу можно решить методом «научного тыка»

Допустим, в какой-то момент малыш Федя обгоняет Соню на ходулях. Отметим это место специальной меткой, как условное начало круга. Как только он обгоняет Соню, он понимает, что (теперь уже) она – впереди него на расстоянии длины круговой дорожки (фактически она почти впритык позади него, но ведь дорожка круговая (!), а значит, Соня, как бы и впереди на расстоянии длины дорожки).

Пускай теперь до нового места встречи Соня пройдёт от метки какую-то часть круговой дорожки, назовём это «кусок дорожки», а малыш Федя до этого нового места встречи проедет на велосипеде целый круг и ещё такую же часть дорожки, т.е. такой же «кусок», как и Соня.

Новое место встречи, таким образом, сместилось от начальной метки на «кусок дорожки».

После второй встречи, Федя опять обгонит Соню и потом опять встретится с ней уже в третий раз со смещением ещё на один «кусок дорожки» от предыдущего места встречи, которое и так уже было смещено от начальной метки на «кусок дорожки», стало быть, третья встреча сместится от начальной метки на «два куска дорожки».

Второе место встречи сместилось от начальной метки
на «кусок дорожки», а Федя проехал лишний круг.

Третье место встречи сместилось от начальной метки
на «два куска дорожки», а Федя проехал два лишних круга.

Четвёртое место встречи сместится от начальной метки
на «три куска дорожки», а Федя проедет три лишних круга.

Пятое место встречи сместится от начальной метки
на «четыре куска дорожки», а Федя проедет четыре лишних круга.

Заметим, что если бы Соня к пятому месту встречи, смещённому от начальной метки на «четыре куска дорожки бы целый круг, то тогда Федя проехал бы 4 лишних круга и ещё «четыре куска дорожки», т.е. такое же расстояние, как и Соня, а значит ещё один добавочный круг.

И в таком случае, получилось бы, что Соня один круг, а Федя проехал пять кругов, что как раз и сходится с их соотношением скорости. Всё правильно, Федя ведь ездит в 5 раз быстрее, а значит, он и должен проехать в 5 раз больше, чем проходит Соня!

Значит, наше предположение верно. К пятой встрече Соня проходит полный круг, а стало быть, она приходит к начальной метке, которую мы отметили в месте первой встречи, т.е. место пятой встречи совпадает с местом первой встречи. Дальнейшие встречи станут совпадать со встречами в первом цикле рассуждений. Таким образом, всего существует 4 разных места, где Федя обгоняет Соню.

Так же, эту задачу можно решить и «аналитически», через введение неизвестного параметра скорости, и рассмотрения относительной скорости участников, т.е. скорости сближения.

Пусть скорость Сони равна v .

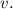Тогда скорость Феди равна 5v .

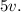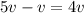Когда Федя догоняет Соню, их скорость сближения равна 5v - v = 4v

(вычитаем, поскольку Соня уходит от догоняющего её Феди, тем самым, как бы мешая ему себя догонять).

Когда Федя в очередной раз обгоняет Соню, его удалённость от Сони, которую он встретит в будущем, в следующем месте обгона, составляет как раз один круг. За время, пока Федя доедет до нового обгона Сони, Соня пройдет по круговой дорожке в 4 раза меньшее расстояние, поскольку её скорость в 4 раза меньше скорости сближения.

Из этого и следует, что за время между двумя очередными последовательными встречами, которые разделяют участников движения расстоянием в один круг, Соня проходит только четверть круговой дорожки. Значит за 4 дополнительные встречи (после первой начальной) она и пройдёт полный круг. Т.е. всего существует 4 места, в которых малыш Федя обгоняет Соню на ходулях.

О т в е т : (б) в 4 точках.

4,8(35 оценок)

Это интересно:

Компьютеры-и-электроника

15.06.2021

Как открыть программу Terminal на Mac...

Компьютеры-и-электроника

01.03.2023

Как войти в Windows со стандартным паролем администратора...

Искусство-и-развлечения

01.04.2021

Как научиться петь: советы для начинающих...

Образование-и-коммуникации