По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие выполняется
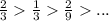
По второму признаку Лейбница предел ряда должен стремится к 0.
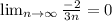
Второе условие Лейбница выполняется. Таким образом, ряд сходится. Исследуем теперь ряд на абсолютной и условной сходимости. Для этого рассмотрим данный ряд по модулю
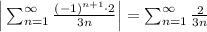
Этот ряд расходится, так как это гармонический ряд и он является расходящимся.
Таким образом, данный исследуемый ряд сходится условно.
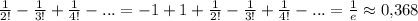
Баланс на 27.07.2012 равен 90
Пошаговое объяснение:
Дата. Расход. Приход. Баланс
01.02.2012. нет 320 =320
05.02.2012 - 185 - =320-185=135
11.02.2012. нет 65 =135+65=200
18.02.2012. -240 - =200-240=-40 ( перерасход)
23.02.2012. нет 270 =-40+270=230
27.07.2012 -140 - =230-140=90
Баланс на 27.07.2012 равен 90 ( ура он положительный, и может на него начисляются проценты)
|a| = √(ax² + ay² + az²)= √(1² + 0² + 2²) = √(1 + 0 + 4) = √5
Найдем направляющие косинусы вектора a:
cos α = ax/|a| = 1/√5 ≈ 0.44721,cos β = ay/|a| = 0/√5 = 0,
cos γ = az/|a| = 2/√5 ≈ 0.89443.
2) Найдем модуль вектора b:
|b| = √(bx² + by² + bz²) = √(1² + (-3)² + 7²) = √(1 + 9 + 49) = √59
Найдем направляющие косинусы вектора b:
cos α = bx/|b| = 1/√59 ≈ 0.130189,cos β = by/ |b|= -3/√5 ≈ -0.390567.
cos γ = bz/|b| = 7/√59 ≈ 0.91132.