Пошаговое объяснение:
Вариант решения по вашему условию:
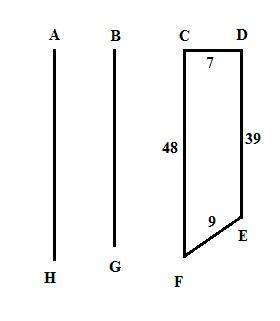
По условию можно сделать лишь такой эскиз решетки (первый рисунок во вложении)
Про связь АH, DG и CF никаких данных нет.
Так как DE≠CF решетка имеет не прямоугольный контур (границу вокруг решетки).
1) По данным не возможно определить метраж прута.
2) Нет никаких данных про эти отрезки
3) 1. Измерил, может, правильно, но не все данные.
2. Ничего не известно про это
Вариант решения по рисунку к задаче (второй во вложении):
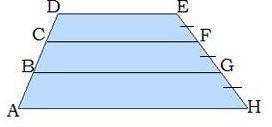
Для решения используем рисунок 3
Рассмотрим DEGB - трапеция.
CF проходит через середину EG (EF=FG) и CF || DE || BG
Отсюда можно сделать вывод, что CF - средняя линия трапеции DEGB
Средняя линия равна половине суммы оснований
CF=(BG+DE)/2 =>
BG=2CF-DE=2*48-39=57 см
Так же так как CF - средняя линия, DC=CB=7 см
Рассмотрим четырехугольник CFHA - это так же трапеция
BG проходит через середину FH (FG=GH) и BG || CF || HA
Отсюда можно сделать вывод, что CF - средняя линия трапеции CFHA
По примеру предыдущей трапеции находим AH:
AH=2BG-CF=2*57-48=66 см
А CB=AC=7 см (как и в предыдущем случае)
Найдем сумму всех отрезков:
1) 39+48+57+66+9*3+7*3=258 см=2,58 м металлического прута
2) BG=57 см
AH=66 см
3) В школе он хорошо освоил геометрию

Рівняння вигляду 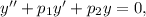 де
де 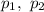 — задані числа, є лінійним однорідним диференціальним рівнянням (ЛОДР) другого порядку зі сталими коефіцієнтами.
— задані числа, є лінійним однорідним диференціальним рівнянням (ЛОДР) другого порядку зі сталими коефіцієнтами.
Метод Ейлера (метод характеристичних рівнянь) дозволяє знаходити загальний розв'язок для вказаного рівняння.
Розв'язок цього рівняння шукаємо у вигляді 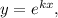 де
де 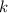 — деяка стала (дійсна чи комплексна). Тоді, якщо
— деяка стала (дійсна чи комплексна). Тоді, якщо 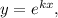 то
то 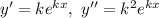
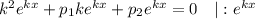
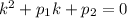 — характеристичне рівняння
— характеристичне рівняння
Можливі три випадки:
➀ 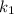 і
і 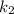 — дійсні,
— дійсні, 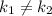
Фундаментальна система розв'язків: 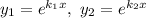 — функції лінійно незалежні, бо
— функції лінійно незалежні, бо 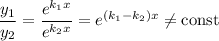
Загальний розв'язок: 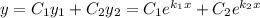
Приклад: а) 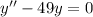
Метод Ейлера: 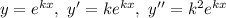
Характеристичне рівняння: 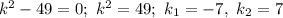
Загальний розв'язок: 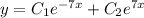
Відповідь: 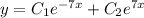
Приклад: в) 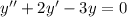
Метод Ейлера: 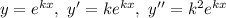
Характеристичне рівняння: 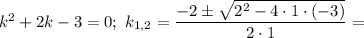
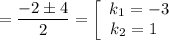
Загальний розв'язок: 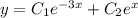
Відповідь: 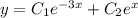
➁ 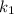 і
і 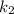 — дійсні,
— дійсні, 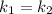
Якщо покласти 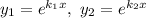 , то ці функції лінійно залежні, бо
, то ці функції лінійно залежні, бо 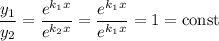
Фундаментальна система розв'язків: 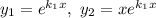 — функції лінійно незалежні, бо
— функції лінійно незалежні, бо 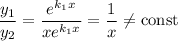
Загальний розв'язок: 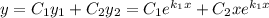
➂ 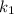 і
і 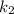 — комплексно спряжені,
— комплексно спряжені, 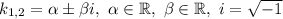
Фундаментальна система розв'язків: 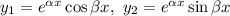 — функції лінійно незалежні, бо
— функції лінійно незалежні, бо 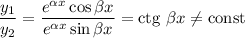
Загальний розв'язок: 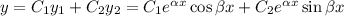
Приклад: б) 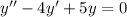
Метод Ейлера: 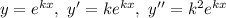
Характеристичне рівняння: 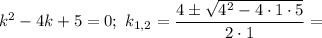
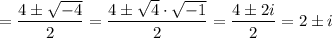
Отже, 
Загальний розв'язок: 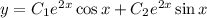
Відповідь: 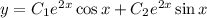
28000 г= 28 кг
7000000 г=7 т
685000 м=685 км
30500 см=305 м
200000 мм=200 м