т.к. площадь трапеции равна полусумме ее оснований на высоту, то
S=4,8*5=24
умножаем на 5 так как это средняя линия, а средняя линия равна полусумме оснований
площадь прямоугольника так же равна 24(по условию)
составим уравнение:
24=((а+b)/2)*4,8
24=(a+b)*2,4
a+b=10
составим систему уравнений:
a+b=10(выразили только что из уравнения для площади трапеции
a*b=24(площадь прямоугольника)
Выразим одну переменную через другую:
a=10-b
Подставим в другое уравнение:
(10-b)*b=24
10b-b^2=24
b^2-10b+24=0
b1=(10-√(100-4*24))/2=4
b2=(10+√(100-4*24))/2=6
Подставляем в первое уравнение:
a1=10-b1=10-4=6
a2=10-b2=10-6=4
ответ: основания равны 6 и 4
Девочек в 6А классе: 9, всего в 6А классе: 15+9=24 человека.
В 6Б классе 16 мальчиков.
Всего в 6Б классе: 18+16=34 человека.
Всего в двух классах учится: 24+34=58 человек.
Девочек больше в 6Б классе на: 18-9=9 человек.
Мальчиков больше всего в 6Б классе на: 16-15=1 человека.
Пошаговое объяснение:
По условию дано, что в 6А классе мальчиков 15 человек и количество мальчиков составляет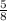 
от общего количества учеников этого класса.
А в 6Б, наоборот, девочек 18 человек, и их количество составляет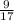 
от всех учеников в этом классе.
Поэтому, для начала найдем количество девочек в 6А классе. У нас получается пропорция:
Если 15 мальчиков и это 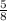от количества учеников
То x девочек, это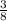 
от количества учеников (оставшаяся часть класса, когда количество всех учеников принято за 1).
Получаем, что девочек в 6А классе: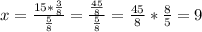 
.
Тогда, всего в 6А классе: 15+9=24 человека.
Разберем количество мальчиков в 6Б классе. У нас получается такая же пропорция:
Если 18 девочек, это 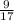от общего количества учеников
То x мальчиков, это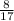 
от количества учеников.
Значит, мальчиков в 6Б классе: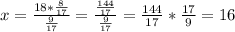 
.
В 6Б классе 16 мальчиков.
Всего в 6Б классе: 18+16=34 человека.
Всего в двух классах учится: 24+34=58 человек.
Девочек больше в 6Б классе на: 18-9=9 человек.
Мальчиков больше всего в 6Б классе на: 16-15=1 человека.
4*8=32 метра потребуется на 8 сукон