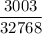
Пошаговое объяснение:
Пусть в каждом гардеробе было по 15 мест, представим гардероб как последовательность нулей и единиц: 0 — школьник разделся в другом гардеробе, 1 — школьник разделся в этом гардеробе. Тогда ситуация выглядит примерно так:
I: 110010100011101
II: 001101011100010
Если в первом гардеробе задана некоторая последовательность, то она однозначно задаёт последовательность второго гардероба. На каждой позиции первого гардероба может быть либо 0, либо 1, поэтому, учитывая однозначность, всего возможных ситуаций 2¹⁵ = 32768.
Если в правом гардеробе занято вдвое мест, чем в левом, то есть вдвое больше единиц, чем в левом (10 в правом, 5 в левом), то искомое количество подходящих ситуаций — число расставить 10 единиц в правом гардеробе.
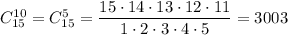
Искомая вероятность равна 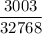 .
.
17640 вариантов
Пошаговое объяснение:
посчитаем отдельно сколько вариантов составить комиссию из членов 1й и 3й, и из членов 2й и 3й:
в 1й и 3й партиях суммарно (5+4)=9 человек, количество вариантов выбрать 5 человек из 9 это 9*8*7*6*5=15120
во 2й и 3й партиях суммарно (3+4)=7 человек, кол-во вариантов выбрать 5 человек из 7 это 7*6*5*4*3=2520
15120 -это количество вариантов составить комиссию только из членов 1й и 2й партий, а 2520 - это количество вариантов составить комиссию только из членов 2й и 3й партий, значит количество разных комиссий которые можно составить, если представители партии №1 и №2 не могут быть ее членами одновременно это 15120+2520=17640
/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/