ответ:1)25:5=5
(25+5):2=60
2) 80*1\8=10
(80+10)*2=180
3)16*4=64
4)12*2=24
Пошаговое объяснение:
на 1 задаче мы 25 делим на 5 получается 5 потом 25 плюсуем к 5 и делим на 5 равно 60
на 2 задаче 80 умнажаем на 1\8 получяем 10 к 80 пристовляем 1 будет 80\1 умножаем на 1\8 равно 10 потому что 1 на 1 укрощяем равно 1 а 8 на 80 украшяем на 10, 80 плюс 1о равно 90 и умножаем на 2 равно 180 потому что когда у оприделенннай цифры есть 0 ну в нашем случае 90 это таже 9 только с 0 когда мы 9 умножаем на 2 у нас же получается 18 но тут мы прибовляем только 0 вот и получился ответ 180
на 3 Если одна четверть равна 16 м, значит вся проволока в 4 раза больше
на 4 в году всего 12 месяцев умножаем в 2 ровно 24 месяца
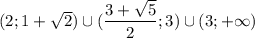
Пошаговое объяснение:
ОДЗ логарифмов: x > 0, x ≠ 1, x > 2, x ≠ 3 ⇒ x > 2, x ≠ 3
Пусть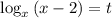 
. Тогда 
:
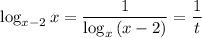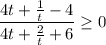. Заметим, что t ≠ 0, так как это значение достигается только при x = 3 (x - 2 = x⁰ = 1 ⇔ x = 3). Но при x = 3 основание логарифма 
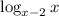равно 1, что не удовлетворяет ОДЗ. Значит, домножим обе части дроби на t:
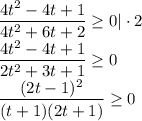
Решим методом интервалов:
+ - + +
----o----o----*---->
-1 -¹/₂ ¹/₂
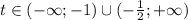
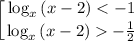
Заметим, что по ОДЗ x > 2, то есть основание логарифма всегда больше 1. Значит, на ОДЗ неравенства равносильны:
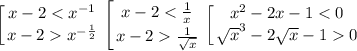
Первое неравенство имеет решение (с учётом ОДЗ)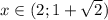 
Второе неравенство раскладывается на множители:
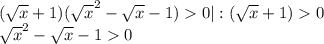
Нули получившегося неравенства: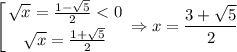 
C учётом ОДЗ получаем, что в данном случае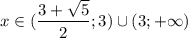 
(левая граница меньше правой, так как √5 < 3).
Объединим промежутки. Сравним правую границу первого неравенства и левую границу второго. Сравним эти числа относительно 2,5:
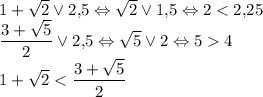
Тогда промежутки не пересекаются, итоговый ответ: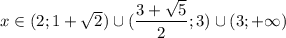 
tg(2Π-60°)*sin(3Π/2 -60°)=-tg60°*(-cos60°)=tg60°*cos60°=sin60°/cos60° * cos60°=sin60°=√3/2
2cos4x-1=0
2cos4x=1
cos4x=1/2
4x=+-Π/3+2Πk, k€Z
x=+-Π/12+Πk/2, k€Z
2cos^2x-9sinx+3=0
2(1-sin^2x)-9sinx+3=0
2sin^2x+9sinx-5=0
Пусть t=sinx, где t€[-1;1], тогда
2t^2+9t-5=0
t1=-5 посторонний
t2=1/2
Вернёмся к замене
sinx=1/2
x1=Π/6+2Πk, k€Z
x2=5Π/6+2Πk, k€Z
a=a°Π/180°=140°Π/180°=7Π/9