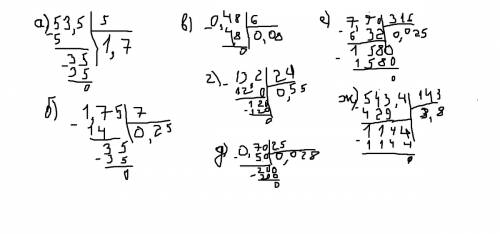
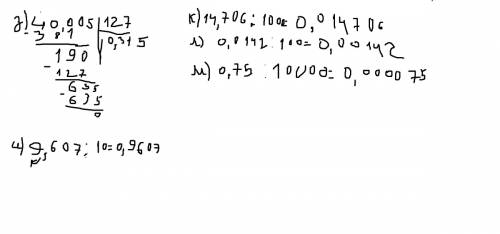
ясно, что двигаясь вниз и вправо, независимо от формы пути, фоксу нужно будет сделать 6 ходов, чтобы из левой верхней клетки попасть в правую нижнюю. из этих шести ходов 3 обязательно будут на одну клетку вниз, а 3 - на одну клетку вправо. поскольку после каждого ходачисло под фишкой меняется, то имеем перестановку из 6 элементов двух разных типов, по три каждого типа. чтобы подсчитать общее количество вариантов достижения правой нижней клетки применяем формулу для числа перестановок n элементов с повторениями:
p = n! / (n1! где n=6; n1=3 и n2=3.
подставляя, получаем
p=6! / (3! 3! )=720/36=20
ответ: 20
б) 0,25
в) 0,08
г) 0,55
д) 0,028
е) 0,025
ж) 3,8
з) 0,315
и)0,9607
к) 0,014706
л) 0,000142
м) 0,000075