Рассуждения в разделе "Пошаговое объяснение".
Пошаговое объяснение:Признаки делимости числа на 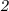 :
:
Число делится на  , если его конечная цифра чётная.
, если его конечная цифра чётная.
Пример: 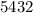 делится на
делится на  , ибо его конечная цифра чётная.
, ибо его конечная цифра чётная.
Признаки делимости числа на 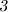 :
:
Число делится на  , если сумма его цифр делится на
, если сумма его цифр делится на  .
.
Пример: 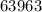 делится на
делится на  , ибо сумма его цифр делится на
, ибо сумма его цифр делится на  .
.
Признаки делимости числа на 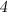 :
:
Число делится на  , если его
, если его  последние цифры нули или образуют число, делящиеся на
последние цифры нули или образуют число, делящиеся на  .
.
Пример: 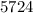 делится на
делится на  , ибо
, ибо  последние цифры (последняя цифра, если число однозначное) образуют число
последние цифры (последняя цифра, если число однозначное) образуют число 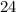 , делящиеся на
, делящиеся на  .
.
Признаки делимости числа на 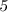 :
:
Число делится на  , если его конечная цифра
, если его конечная цифра 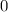 или
или  .
.
Пример: 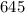 делится на
делится на  , ибо его конечная цифра
, ибо его конечная цифра  .
.
Признаки делимости числа на 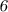 :
:
Число делится на 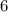 , если конечная цифра чётная и сумма цифр этого числа делится на
, если конечная цифра чётная и сумма цифр этого числа делится на  .
.
Пример: 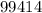 делится на
делится на 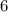 , ибо его конечная цифра
, ибо его конечная цифра  чётная и сумма цифр этого числа делится на
чётная и сумма цифр этого числа делится на  .
.
Признаки делимости числа на 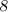 :
:
Число делится на 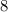 , если
, если  его последние цифры образуют число, делящиеся на
его последние цифры образуют число, делящиеся на 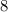 .
.
Пример: 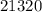 делится на
делится на 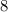 , ибо
, ибо  его последние цифры образуют число
его последние цифры образуют число 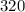 , делящиеся на
, делящиеся на 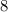 .
.
Признаки делимости числа на 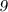 :
:
Число делится на 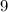 , если сумма его цифр делится на
, если сумма его цифр делится на 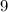 .
.
Пример: 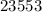 делится на
делится на 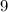 , ибо сумма его цифр делится на
, ибо сумма его цифр делится на 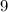 .
.
Признаки делимости числа на  :
:
Число делится на 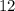 , если оно кратно
, если оно кратно  и
и  .
.
Пример: 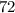 делится на
делится на 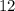 , ибо оно кратно
, ибо оно кратно  и
и  .
.
Признаки делимости числа на 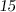 :
:
Число делится на 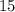 , если его конечная цифра
, если его конечная цифра 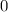 или
или  и сумма цифр этого числа делится на
и сумма цифр этого числа делится на  .
.
Пример: 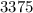 делится на
делится на 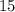 , ибо его конечная цифра
, ибо его конечная цифра  и сумма цифр этого числа делится на
и сумма цифр этого числа делится на  .
.
------------------------------------------------------------------------------------------------
Какие из чисел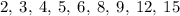 являются делителем
являются делителем 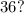
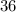 делится на
делится на 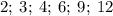 , ибо его конечная цифра чётная, сумма цифр этого числа делится на
, ибо его конечная цифра чётная, сумма цифр этого числа делится на  и
и 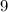 , оно кратно
, оно кратно  и
и  , его
, его  последние цифры образуют число, делящиеся на
последние цифры образуют число, делящиеся на  .
.
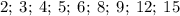 являются кратным
являются кратным 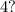
Справедливо неравенство: 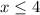 .
.
Числа 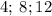 кратны
кратны  , ибо последняя цифра
, ибо последняя цифра 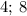 делится/
делится/ последние цифры
последние цифры 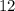 делятся на
делятся на  .
.
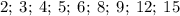 являются делителем
являются делителем 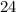 и
и 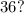
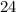 и
и 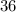 одновременно делятся на
одновременно делятся на 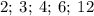 , ибо их конечные цифры чётные, суммы цифр этих чисел делятся на
, ибо их конечные цифры чётные, суммы цифр этих чисел делятся на  , их
, их  последние цифры образуют числа, делящиеся на
последние цифры образуют числа, делящиеся на  .
.
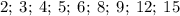 являются делителем
являются делителем 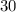 и кратным
и кратным 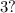
Требования к заданию: 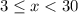 , где
, где  - искомые числа. Число
- искомые числа. Число  уже не подходит.
уже не подходит.
Числа 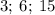 являются делителями
являются делителями 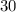 и кратны
и кратны  , ибо сумма цифр числа
, ибо сумма цифр числа 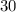 делится на
делится на  , последняя цифра
, последняя цифра 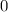 и она чётная.
и она чётная.
= 124 м
или
2 * 30 + 2 * 20 + 2 * 12 = 60 + 40 + 24 = 124 м