Пошаговое объяснение:
Базис. Векторы a и b образуют базис, поскольку на плоскости (у векторов по две координаты) любые два линейно независимых вектора образуют базис (поскольку пространство двумерно), а линейная независимость на плоскости эквивалентна условию, что векторы непараллельны, т.е. их координаты непропорциональны. Впрочем, можно подойти и формально, записав линейную комбинацию векторов a и b, а также приравняв её к нулю:
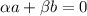
![\left[\begin{array}{cc}3&1\\5&-7\end{array}\right] * \left[\begin{array}{c}\alpha \\\beta \end{array}\right] = \left[\begin{array}{c}0\\0 \end{array}\right]](/tpl/images/4789/5603/bdaee.png)
где 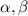 - числа. В силу того, что определитель матрицы векторов не равен нулю (матрица невырожденная), существует только нулевое решение, что означает линейную независимость векторов a и b.
- числа. В силу того, что определитель матрицы векторов не равен нулю (матрица невырожденная), существует только нулевое решение, что означает линейную независимость векторов a и b.
Разложение. Чтобы найти разложение вектора c по базису, приравняем линейную комбинацию векторов a и b к вектору c:
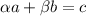
![\left[\begin{array}{cc}3&1\\5&-7\end{array}\right] * \left[\begin{array}{c}\alpha \\\beta \end{array}\right] = \left[\begin{array}{c}7\\3 \end{array}\right]](/tpl/images/4789/5603/5ff81.png)
Домножим левую и правую часть слева на обратную матрицу коэффициентов векторов:
![E*\left[\begin{array}{c}\alpha \\\beta \end{array}\right] =\left[\begin{array}{cc}3&1\\5&-7\end{array}\right]^{-1} * \left[\begin{array}{c}7\\3 \end{array}\right]](/tpl/images/4789/5603/30300.png)
Е - единичная матрица, можно опустить (получается при перемножении матрицы и обратной к ней).
![\left[\begin{array}{cc}3&1\\5&-7\end{array}\right]^{-1} = \left[\begin{array}{cc}\frac{7}{26} &\frac{1}{26} \\\frac{5}{26} &-\frac{3}{26} \end{array}\right]](/tpl/images/4789/5603/2cc1b.png)
![\left[\begin{array}{cc}3&1\\5&-7\end{array}\right]^{-1} * \left[\begin{array}{c}7\\3 \end{array}\right] = \left[\begin{array}{cc}\frac{7}{26} &\frac{1}{26} \\\frac{5}{26} &-\frac{3}{26} \end{array}\right]* \left[\begin{array}{c}7\\3 \end{array}\right] = \left[\begin{array}{c}2\\1\end{array}\right] = \left[\begin{array}{c}\alpha \\\beta \end{array}\right]](/tpl/images/4789/5603/ede93.png)
Итак,
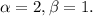
Значит, 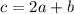 .
.
Прямой проверкой можно убедиться в правильности ответа:
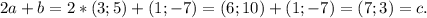
В решении.
Пошаговое объяснение:
Наташа и Оля учатся в кулинарном колледже. Они изучают технологии приготовления различных блюд.
На занятиях по теме «Каши и блюда из круп» при вычислении массы готового продукта учащиеся считают, что:
- одна порция – это 200 граммов готовой каши;
- из 1 кг пшённой крупы получается 4 кг готовой каши;
- для приготовления 1 кг готовой каши пшённой необходимо 800 мл жидкости, из которой 40 % составляет вода и 60 % молоко.
1) 800 : 100% * 40% = 320 (мл) - вода;
2) 800 : 100 * 60 = 480 (мл) - молоко.
а) 0,5×82/5-1/2÷5/7=1/2×82/5-1/2÷5/7=41/7-7/10=15/2
6,4+0,9÷1,5=6,4÷0,6=7
б)0,75+0,5-3/8=0,75+0,5-0,375=0,875
1 5/12 - 9/16 + 1 1/3=5/4-9/16+11/3=60/48-27/48+176/48=209/48
в)12,8 × 3,75 - 4 4/11 × 4 1/8=64/5×15/4×4×41,8=16×3×4×41/8=2×3×4×41=984
11 2/3: 7/18=11 2/3÷18/7=16,6=96