1). Строим произвольный прямоугольный треугольник АСВ. ∠АСВ = 90°.
В этом треугольнике - два острых угла: ∠САВ и ∠СВА.
Докажем, что сумма ∠САВ + ∠СВА = 90°.
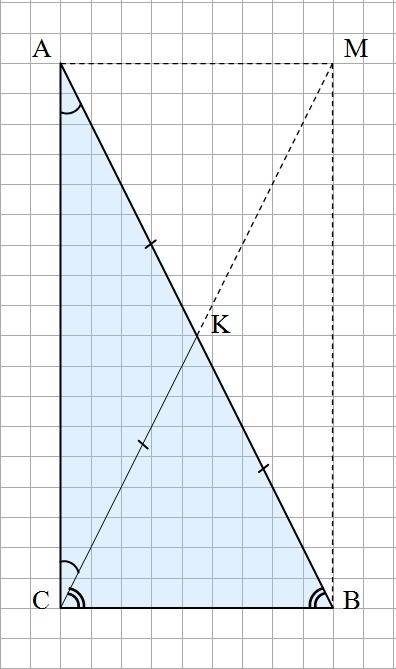
2). Достраиваем треугольник АСВ до прямоугольника АМВС.
Диагонали прямоугольника равны и делятся точкой пересечения пополам. Тогда: АК = КВ = СК и СК - медиана ΔСАВ, проведенная к гипотенузе.
Образовались два равнобедренных треугольника: ΔАКС и ΔСКВ.
В ΔАКС: АК = СК => ∠КСА = ∠САК. (1)
В ΔСКВ: СК = КВ => ∠КСВ = ∠КВС. (2)
Так как в ΔАСВ прямой угол ∠АСВ = ∠КСА + ∠КСВ = 90°.
Учитывая (1) и (2), получим: ∠АСВ = ∠САК + ∠КВС = 90°.
Что и требовалось доказать.
1) Чтобы не запутаться, обозначим скорость на велосипеде через В км/час, а скорость пешком через П км/час. 90 км турист проехал на велосипеде, значит, время, которое он затратил на это, равно 90/В. 10 км он шел пешком, потратив на это времени 10/П. Так как на езду на велосипеде потрачено на 4 часа больше, то можем составить первое уравнение: 90/П - 10/В = 4
2) Из условия задачи, а именно: "Ящо б турист йшов пішки стільки часу скільки їхав велосипедом,а їхав велосипедом стільки скільки ішов пішки,то відстані які він пройшов пішки і проїхав велосипедом, були б одинакові. " составляем второе уравнение:
П*(90/В) = В*(10/П)
Преобразуем это уравнение, избавляясь от дроби:
90П² = 10В²
9П² = В²
В = 3П
3) Подставляем значение В в первое уравнение, получаем:
90/3П - 10/П = 4
30/П - 10/П = 4
20/П = 4
П = 5 км/час - это скорость пешком.
Тогда скорость на велосипеде равна В = 3П = 3*5 = 15 км/час
4) Время, которое ехал турист на велосипеде равно:
90/В = 90/15 = 6
ответ: 6 часов.