v=800 км/ч
t=1 ч
S-?
S=vt
S=800*1=800 км
Ну это если самолет падать не будет. Если будет падать, то на 10 км больше.
Пошаговое объяснение:
Далее выясняется, что самолет летит по экватору на высоте 10 км
Это немного другая задача. Нужно знать путь, который надо пролететь. Допустим это 40075км экватора (на 0км над Землей), но мы летим на 10км и этот путь будет больше. Насколько больше?
S=2*Pi*R
R=S/2*Pi
А при R2=R+10 ,будет
S2=2*Pi*(S/2*Pi+10)=S+Pi*20 - всего-то увеличится на 62.8 км и будет 40137.8 км.
Кстати вот на этот интересный факт надо обратить внимание. Что при изменении радиуса на x периметр круга изменяется на 2Pi*x.
Затем это надо поделить на скорость 800 км/ч и получишь результат.
40137.8/800≈50,17 ч
Т.е. за чуть более 2х суток можно долететь до точки назначения (откуда вылетел).
Но в следующий раз лучше писать сразу нужную задачу. Всю.
они встретятся через 2,4 часа.
Пошаговое объяснение:
Задача на встречное движение.
Однако, в условии не указано не расстояние, ни скорость, только время.
Поэтому будем отталкиваться от времени и определяться со скоростью и расстоянием в условных частях.
Итак.
Если мотоциклист тратит на весь путь 4 часа, а велосипедист 6 часов, то значит скорость мотоциклиста в 1,5 раза больше скорости велосипедиста. (6 : 4 = 1,5)
Тогда и путь мотоциклист до встречи проедет а 1,5 раза больше.
Т.е. если велосипедист проедет 1 часть пути, то мотоциклист за такое же время проедет 1,5 часть пути.
Тогда у нас получится, что весь путь составляет 2,5 условных частей.
И если мы принимаем весь путь за 1 (один путь), то путь разделится между мотоциклистом и велосипедистом в отношении 1,5 : 1.
Т.е мотоциклист проедет 0,6 части пути (1,5 : 2,5) до встречи, а велосипедист 0,4 части пути (1 : 2,5).
Теперь можем составить пропорцию для мотоциклиста
1 путь - за 4 часа
0,6 часть пути - за х часов
по правилу пропорции получим
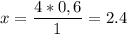 (часа)
(часа)
Для проверки можем составить такую же пропорцию и для велосипедиста
1 путь - за 6 часов
0,4 часть пути - за х часов
Тогда велосипедист до встречи проедет
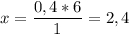 (часа)
(часа)
Таким образом, они встретятся через 2,4 часа.