– каждому действительному простому корню b соответствует частное решение вида
eᵇˣ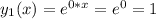
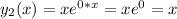
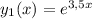
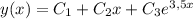
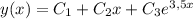
– каждому действительному простому корню b соответствует частное решение вида
eᵇˣ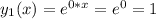
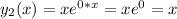
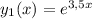
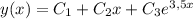
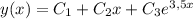
60:2=30 м за 10с
40-30=10м
у Саши на 10 м скорость больше