Пусть все 290 слагаемых равны по 2. Тогда их сумма равна 290·2=580, что меньше 2020. Значит, среди слагаемых есть число, большее 2.
Пусть каждое из 290 слагаемых равно по 2 или по 3. Тогда максимальная сумма, даваемая с таких слагаемых равна 290·3=870, что меньше 2020. Значит, среди слагаемых есть число, большее 3.
Пусть каждое из 290 слагаемых равно по 2, по 3 или по 5. Тогда максимальная сумма, даваемая с таких слагаемых равна 290·5=1450, что меньше 2020. Значит, среди слагаемых есть число, большее 5.
Пусть каждое из 290 слагаемых равно по 2, по 3, по 5 или по 7. Тогда максимальная сумма, даваемая с таких слагаемых равна 290·7=2030. Это больше, чем 2020, значит такой вариант можно рассматривать далее.
Максимальная сумма получается при суммировании 290 чисел, каждое из которых равно по 7. Как видно, максимальная сумма больше требуемой на 10. Тогда, можно уменьшить некоторые слагаемые в этой сумме. Например, уменьшить 2 слагаемых на 5. Получим сумму вида:
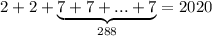
Наибольшим слагаемым является число 7.
ответ: 7
ответ: (Г) 15
1. Всего у нас 3 Феди (больше нет)
если бы мальчиков было 9,то 3 Феди составляют как раз ровно 1/3 от 9 (9*1/3 = 3),
но Федь у нас больше, чем 1/3,
значит мальчиков меньше, чем 9 - максимум 8 (нам же нужно взять самое большое целое число, которое подходит)
2. Мальчиков у нас 8
если девочек 8 - то мальчиков - ровно половина от всего количества - а нам нужно ,чтобы их было больше, значит, девочек должно быть меньше, чем 8 - максимум 7 (опять берем самое большое целое число, подходящее к задаче)
3. Итого 7 девочек + 8 мальчиков = 15 гостей
4. проверяем.
Допустим у нас не 15, а 16 гостей - делим на две части, но так ,чтобы мальчиков было больше, получаем 7+9=16.Т.е. мальчиков 9.
Федь должно быть больше одной трети. Одна треть от 9 - это 3,
значит, Федь должно быть больше 3х - но это не так - по задачке их ровно 3, значит, 16 не подходит.
1) 1/4+7/12=3/12+7/12=10/12=5/6
2) 3/7×5/6=1/7×5/2=5/14