Даны координаты вершин треугольника ABC:
А (-12; -1), В (0; -10), С (4; 12).
Найти:
1) длина стороны AB = √((0-(-12))² +(-10-(-1)²) = √(144 + 81) = 15.
2) уравнение линии AB. Вектор AВ = (12; -9).
Уравнение AВ: (х + 12)/12 = (у + 12)/(-9) каноническое.
Угловой коэффициент к = -9/612= -3/4.
3) Уравнение высоты CD, проведенной из точки C;
Это перпендикуляр к стороне AB.
к(CD) = -1/(к(AВ) = -1/(-3/4) = 4/3.
Уравнение CD: у = (4/3)х + в. Для определения слагаемого в подставим координаты точки C.
12 = (4/3)*4 + в, отсюда в = 12 - (16/3) = 20/3.
Получаем CD: у = (4/3)х + (20/3).
4) Длина высоты CD.
По одному из вариантов:
1. Площадь треугольника ABC
S=(1/2)*|(Хв-Ха)*(Ус-Уа)-(Хс-Ха)*(Ув-Уа)| = 150.
2. CD = 2S/|AB| = 2*150/15 = 20.
5) Уравнение медианы АЕ.
Точка Е - середина ВС. Е(2; 1).
Вектор АЕ = √((2-(-12)) +( 1-(-1)) = (14; 2).
Уравнение медианы АЕ: (x + 12)/14 = (y + 1)/2 или в общем виде
x - 7y + 5 = 0.
ответ: ≈14,51 см
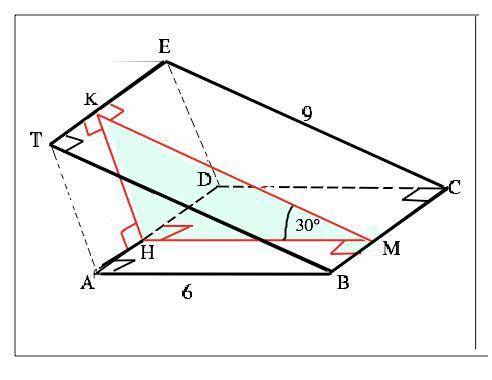
Пошаговое объяснение: Угол между плоскостями – двугранный угол. Его величина определяется градусной мерой линейного угла, сторонами которого являются лучи, проведённые в его гранях перпендикулярно ребру с общим началом на нём.
Обозначим квадрат АВСD, прямоугольник ТВСЕ. Ребром угла между их плоскостями является их общая сторона ВС.
КМ⊥ВС, МН⊥ВС. Плоскость, содержащая угол 30°, перпендикулярна плоскостям обеих граней.
АD║ВС, ТЕ║ВС ⇒ ТЕ║AD. Искомое расстояние - длина отрезка КН между ними.
Длина общей стороны ВС данных фигур - сторона квадрата, поэтому ВС=√S=√36=6 см. НМ=АВ=6 см, КМ=ТВ=9 см. т.к. параллельны им и пересекаются с противоположными сторонами прямоугольников под прямым углом.
По т.косинусов КН²=КМ²+НМ*-2КМ•НМ•cos30°
КН²=36+81-2•6•9•√3/2, откуда КН=√(117-54√3)=≈14,51 см
б) cos(