Пошаговое объяснение:
Среднее арифметическое трёх чисел равно 1,54.
Первое число больше второго числа в 2 раз.
Третье число меньше второго на 0,18.
Найди первое, второе и третье число.
Решение.
Средним арифметическим нескольких чисел называют частное от деления суммы этих чисел на количество слагаемых.
Пусть третье число равно х.
Тогда второе число равно (х +0,18).
Первое число равно ((х +0,18) * 2).
Зная, что среднее арифметическое трёх чисел равно 1,54 - составим уравнение:
(((х +0,18) * 2) + (х +0,18) + х) : 3 = 1,54
((х +0,18) * 2 + х +0,18 + х) : 3 = 1,54
(2х + 0,36 + х + 0,18 + х) : 3 = 1,54
(4х + 0,54) : 3 = 1,54
4х + 0,54 = 1,54 *3
4х + 0,54= 4,62
4х = 4,62 – 0,54
4х = 4,08
х = 4,08 : 4
х = 1,02
Третье число равно 1,02
Второе число равно 1,02 + 0,18 = 1,2
Первое число равно 1,2 * 2 = 2,4
Проверка:
(2,4 + 1,2 + 1,02) : 3 = 4,62 : 3 = 1,54
Первое число равно 2,4
Второе число равно 1,2
Третье число равно 1,02
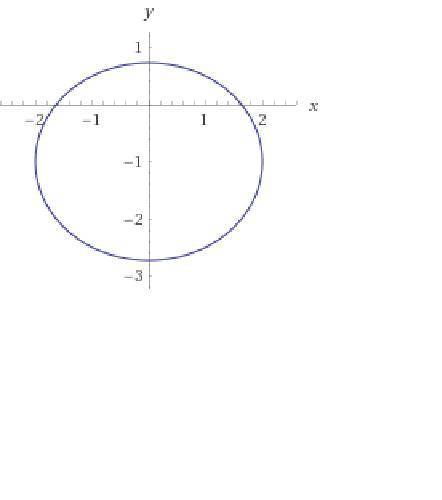
По условию задания составим уравнение расстояния произвольной точки М(х; у) от точки P(1; -1) в 2 раза меньшего, чем от точки М до прямой х = 4.
√((x-1)² + (y + 1)²) = |4 - x)|/2.
Модуль в правой части взят, чтобы длина не была отрицательной для точек, расположенных левее оси Оу.
Возведём обе части в квадрат.
x² - 2x + 1 + (y + 1)² = (16 - 8x + x²)/4,
4x² - 8x + 4 + 4(y + 1)² = 16 - 8x + x²,
Приведём подобные: 3x² + 4(y + 1)² = 12.
Разделим обе части на 12.
(3x²/12) + (4(y + 1)²)/12 = 1. Приведём к каноническому виду.
(x²/2²) + ((y + 1)²)/(√3)²) = 1.
Получено искомое уравнение. Это уравнение эллипса.
Центр её расположен в точке (0; -15).
Полуоси: действительная равна а =2, мнимая b = √3.
Найдем координаты ее фокусов: F1(-c;0) и F2(c;0), где c - половина расстояния между фокусами
Определим параметр c: c² = a² - b² = 4 - 3 = 1 .
c = √1 = 1.
Тогда эксцентриситет будет равен: е = с/а = 1/2 .
2) 8/45*3 = 24/45 = 8/15
3) 3/5 + 8/15 = (9+8)/15 = 17/15
4) 7/24-9/40 = (280 - 216)/ 960 = 64/960 = 1/15
5) 17/15:1/15 = 17