Имеем многочлен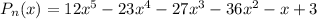 
Корнями многочлена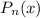 
называют корни уравнения
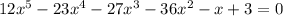
Имеем уравнение пятого порядка. Попробуем его решить с теоремы Безу.
Суть этой теоремы в том, что если уравнение вида с ненулевым свободным членом имеет некий корень , принадлежащий к множеству целых чисел, то этот корень будет делителем свободного члена.
Выпишем все делители свободного члена: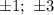 
Подставим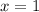 
в корень уравнения и получим:
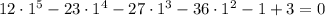
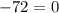— неправда
Подставим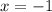 
в корень уравнения и получим:
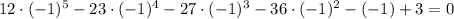
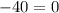— неправда
Подставим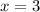 
в корень уравнения и получим:
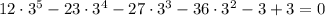
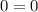— правда
Следовательно,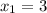 
— один из корней уравнения. Теперь необходимо выполнить деление многочлена столбиком на 
(см. вложение).
После этого исходное уравнение можно записать разложив на множители:
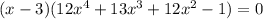
Решаем второе уравнение:
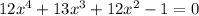
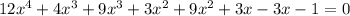
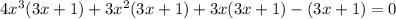
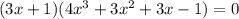
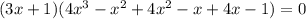
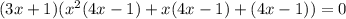
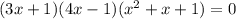
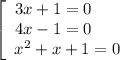
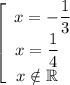
Рациональные корни: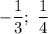 
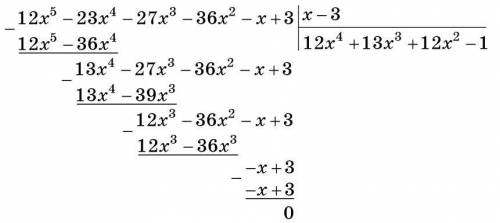
Имеем многочлен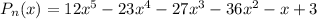
Корнями многочлена 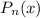называют корни уравнения
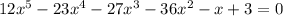
Имеем уравнение пятого порядка. Попробуем его решить с теоремы Безу.
Суть этой теоремы в том, что если уравнение вида с ненулевым свободным членом имеет некий корень , принадлежащий к множеству целых чисел, то этот корень будет делителем свободного члена.
Выпишем все делители свободного члена: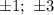
Подставим 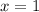в корень уравнения и получим:
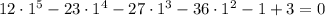
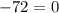— неправда
Подставим 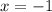в корень уравнения и получим:
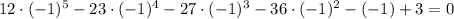
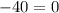— неправда
Подставим 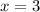в корень уравнения и получим:
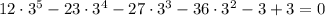
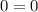— правда
Следовательно, 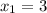— один из корней уравнения. Теперь необходимо выполнить деление многочлена столбиком на (см. вложение).
После этого исходное уравнение можно записать разложив на множители:
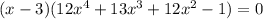
Решаем второе уравнение:
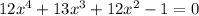
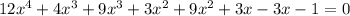
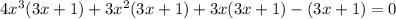
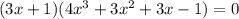
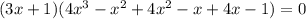
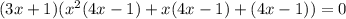
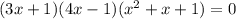
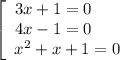
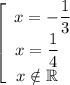
Рациональные корни: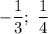
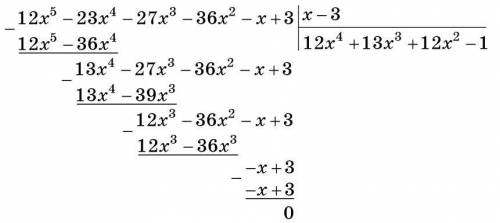
ответ: 47 дней.
Пошаговое объяснение:
Пусть S - площадь поверхности озера, S0 - площадь одной кувшинки. Пусть в первый день в пруду было x шт. кувшинок, тогда во второй день их стало 2*x шт., в третий - 4*x шт., в n-й - 2ⁿ⁻¹*x шт. По условию, S0*2⁴⁸⁻¹*x=S0*2⁴⁷*x=S. Половина площади озера равна S/2. Так как S0*2⁴⁷*x=S, то S/2=S0*2⁴⁷*x/2=S0*2⁴⁶*x. Отсюда следует, что для покрытия кувшинками половины пруда требуется 46+1=47 дней.