ДАНО
Y=(x²-4)/(x²+1)
ИССЛЕДОВАНИЕ
1.Область определения D(x) - непрерывная Х∈(-∞;+∞).
Вертикальных асимптот - нет.
2. Пересечение с осью Х. x = 0. В числителе - (x² - 4) = (x-2)*(x +2) = 0
x1 = -2, x2 = 2
3. Пересечение с осью У. У(0) = -4.
4. Поведение на бесконечности.
\lim_{n \to \infty} \frac{x^2-4}{x^2+1}= \frac{1-0}{1+0}=1limn→∞x2+1x2−4=1+01−0=1
Горизонтальная асимптота - Y = 1.
5. Исследование на чётность.Y(-x) = Y(x). Функция чётная.
6. Производная функции.
Y'(x)= \frac{2x}{x^2+1}- \frac{2x*(x^2-4)}{(x^2+1)^2}=0Y′(x)=x2+12x−(x2+1)22x∗(x2−4)=0
7. Локальные экстремумы.
Максимума - нет, минимум – Ymin(0) = -4.
8. Интервалы монотонности.
Убывает - Х∈(-∞;0]. Возрастает - Х∈[0;+∞)
9. Вторая производная - Y"(x).
Корни производной - точки перегиба: х1 =-√3/3, х3=√3/3. (≈0.58)
9. Выпуклая “горка» Х∈(-∞;-√3/3)∪(√3/3;+∞),
Вогнутая – «ложка» Х∈(-√3/3;√3/3).
10. Область значений Е(у) У∈(-4;1)
11. График в приложении
(x-1,25) / -3 = y / 4 = (z-0,25) / 5
Пошаговое объяснение:
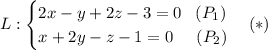
Для построения канонического уравнения прямой необходимо и достаточно знать ее направляющий вектор q и какую угодно точку на этой прямой. Искомая прямая L задана как пересечение плоскостей P_1 и P_2, то есть она лежит в обеих плоскостях. Тогда нормальные векторы каждой плоскости, будучи перпендикулярны к "своим" плоскостям, будут перпендикулярны и к любой прямой, лежащей в "своей" плоскости, в том числе и к L. Другими словами, L перпендикулярна нормальному вектору как P_1, так и P_2. А значит, ее направляющий вектор является векторным произведением нормальных векторов P_1 и P_2
Координаты нормального вектора плоскости — коэффициенты при x, y и z в общем уравнении этой плоскости:
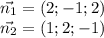
Их векторное произведение найдем, вычислив определитель:
![[\vec{n_1}, \vec{n_2}]=\begin{vmatrix} \vec{i}&\vec{j}&\vec{k}\\2&-1&2\\1&2&-1\end{vmatrix}=\vec{i}\begin{vmatrix} -1&2\\2&-1\end{vmatrix}-\vec{j}\begin{vmatrix} 2&2\\1&-1\end{vmatrix}+\vec{k}\begin{vmatrix} 2&-1\\1&2\end{vmatrix}=\\(-1*(-1)-2*2)\vec{i}-(2*(-1)-1*2)\vec{j}+(2*2-1*(-1))\vec{k}=\\(1-4)\vec{i}-(-2-2)\vec{j}+(4+1)\vec{k}=-3\vec{i}+4\vec{j}+5\vec{k}=(-3;4;5)=\vec{q}](/tpl/images/2007/9668/cc8e6.png)
В качестве точки на L возьмем частное решение системы (*). Пускай y = 0, тогда
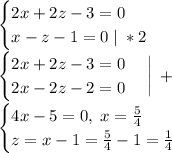
Получили, что искомой прямой принадлежит точка A(1,25; 0; 0,25)
Осталось "собрать" полученную информацию в каноническое уравнение. Оно имеет вид
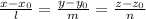 ,
,
где A(x_0; y_0; z_0) и q(l; m; n;). Подставим:
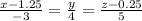
— окончательный ответ
10000+8000=18000
18000/4=4500
4500*2=9000
9000+18000=27000
30000-27000=3000
3000/1500=2
ответ 2 мороженых