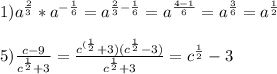
3)
√(5-x²)-3x=0
√(5-x²)=3x
Найдём ОДЗ (область допустимых значений):
а) Выражение под знаком квадратного корня не может быть отрицательным,значит.оно больше или равно 0.
в) В правой части не может стоять отрицательное значение,так как квадратный корень из числа есть число неотрицательное,значит,x≥0.
Решаем систему:
{5-x²≥0 {x²≤5 {-√5≤ x ≤ +√5 ⇒ ОДЗ : 0 ≤ x ≤√5
{3x≥0 {x≥0 {x≥0
Теперь,когда и правая,и левая части у нас положительные,можем возвести их в квадрат:
(√(5-х²)²=(3х)²
5-х²=9х²
9х²+х²=5
10х²=5
х²=0.5
х1=√0.5 >0, но <√5 -значит, х1 -корень уравнения
х2= -√0.5 -не удовлетворяет ОДЗ: 0 ≤ x ≤ √5
ответ: х=√0.5.
------------------------------------------------------------
Если вам удобнее проверить корни,подставив их значения в уравнение,то так тоже можно.
n^4+2*n^3-n^2-2n+1
(n-1)*(n+2)+1=n*n+n-1
(n*n+n-1)^2=n^4+2*n^3-n^2-2n+1
Таким образом, данное выражение равно:
(n*n+n-1)^2
т.е. является квадратом целого числа.