1.
1) 141
2) 45
3) 0,07
4) 12
5) - 0,018
2.
1) 3^14 : 3^12 = 3^2 = 9
2) 29^12 * 29^6 / 29^16 = 29^18 / 29^16 = 29^2 = 841
3) 5^21 / 5^20 = 5
4) 8^14 * 8^24 / 8^36 = 8^38 / 8^36 = 8^2 = 16
5) 9^5 * 81^6 / 3^30 = (3^2)^5 * (3^4)^6 / 3^30 = 3^10 * 3^24 / 3^30 =3^4 = 81
Пошаговое объяснение:
если ты умножаешь отрицательное число на отрицательное то ответ получается без минуса
при умножении одинаковых чисел в степени, степени складываются, а при делении, вычитаются
при возведении степени в степень, степени перемножаются
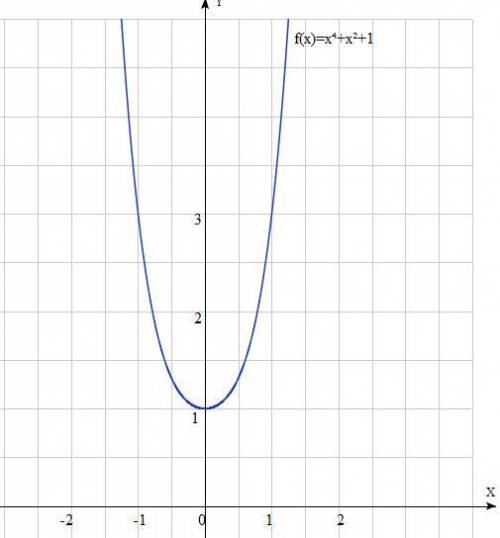
Исследовать функцию и построить график
f(x)=x⁴+x²+1
Пошаговое объяснение:
f(x)=x⁴+x²+1 . Область определения х-любое.
1)Промежутки возрастания и убывания.
Найдем производную функции f'(x)=(x⁴+x²+1)'=4х³+2х=2х(2х²+1).
f'(x)=0 , выражение 2х²+1>0 при любом х.
Критическая точка х=0 .
Если производная функции y=f(x) положительна для любого x из интервала X, то функция возрастает на X,
2х(2х²+1)>0 или х>0
----------------------(0)++++++++ , х∈(0;+∞) .
Т.к. функция определена и непрерывна при любом х, то можно включит концы отрезка х∈ [0;+∞)
Если производная функции y=f(x) отрицательна для любого x из интервала X, то функция убывает на X.
Используя схему выше ⇒ х∈(-∞;0] .
2)Экстремумы.
Точка х₀-точка максимума , если производная меняет свой знак с +на -.
Точка х₀- точка минимума , если производная меняет свой знак с - на +.
у' - +
--------------------------(0)---------------
у убыв min возр
х=0 точка минимума , f(0)=0⁴+0²+1=1
Функция четная f(-x)=(-x)⁴+(-x)²+1=x⁴+x²+1=f(x), график симметричен относительно оси оу.
Доп. точки
х -1,5 -1 -0,5
у 8,31 3 1,31
7x-2x=12-13
5x=-1
x=-5
б)2(x-5)+3=x
2x-10+3=x
2x-x=10-3
x=7